応用数値解析:微分・積分・求根アルゴリズム
• 各課題につき、
• jlファイルを全て提出してください。
• 重要な出力画面 & グラフは,
1. Numerical analysis: 数値解析について
• 数値解析は代数的な方法で解けない問題を、数値データを用いて近似的に解く手法である。
• 詳細の紹介はこちら(Wikipedia)
問題例:多次元方程式
\[ ax^2 + bx + c = 0, ~~a\ne 0 \]
• \(a, b, c\) は係数(Coefficient)
二次方程式の一般解の公式
\[ x = \frac{-b \pm \sqrt{b^{2} - 4ac}}{2a} \]
• 4次方程式までは一般解の公式があり、代数的に解ける。
• 5次方程式以降は、任意の係数に対する一般解の公式が存在しない。
• 一般的に代数的に解けない。
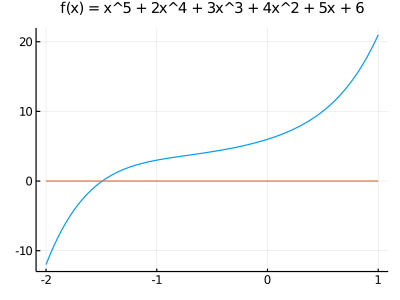
例
\[ x^5 + 2x^4 + 3x^3 + 4x^2 + 5x + 6 = 0\]
微積分
\[ \int (3x^2 + 2x + 1)~dx = x^3 + x^2 + x + C\]
\[ \int e^{-x}~dx = -e^{-x} + C\]
\[ \int \cos(x)~dx = \sin(x) + C\]
\[ \int \sqrt{1 + \cos^2(x) } ~dx \]
\[ \int e^{-x^2}~dx \]
2. 復習:微分
定義
• dy/dx の定義:
\[ \frac{dy}{dx} = \lim_{\Delta x\to0} \frac{\Delta y}{\Delta x} \]
• dy/dx の定義:
\[ \frac{dy}{dx} = \lim_{\Delta x\to0} \frac{\Delta y}{\Delta x} \]
\[ y = f(x) \]
\[ \frac{dy}{dx} = f^{\prime}(x) = \lim_{\Delta x\to0} \frac{f(x + \Delta x)-f(x)}{\Delta x} \]
傾き・勾配との関係
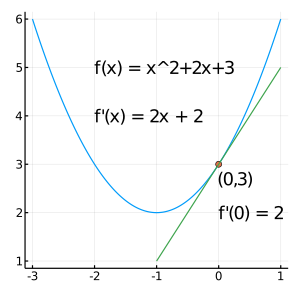
例:
\[ f(x) = x^2 + 2x + 3\]
傾きは
\[ 傾き = \frac{\Delta y}{\Delta x}=f^\prime(x) = 2x + 2\]
3. 復習:積分
定義
\[ \frac{dy}{dx} = f^{\prime}(x) = g(x)\]
\[ y = f(x) = \int g(x) ~dx\]
面積との関係
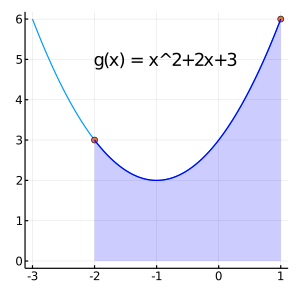
• Area under a curve
• 関数の定積分は、そのグラフによって囲まれる領域の符号付面積として表すことができる。
例1:
\[ g(x) = x^2 + 2x + 3\]
\[ \int_a^b g(x) = \begin{bmatrix}\frac{1}{3}x^3 + x^2 + 3x \end{bmatrix}_a^b\]
例2:
\[ \int_a^b \cos(x) ~dx = \begin{bmatrix} \sin(x) \end{bmatrix}_a^b \]
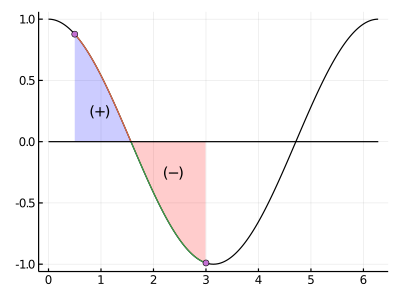
上記の場合\( \int_{0.5}^3 \cos(x) ~dx = \sin(3) - \sin(0.5) = -0.338\)
4. 数値積分
一番単純の方法:
\[ \int f(x) ~dx \approx \sum_{i=1}^n f(x_i)\Delta x_i \]
Δx が一定の場合:
\[ \int f(x) ~dx \approx \Delta x \sum_{i=1}^n f(x_i) \]
練習:代数で解ける例で検証
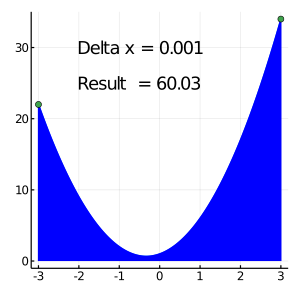
\[ \int_{-3}^3 3x^2 + 2x + 1 ~dx = \begin{bmatrix} x^3 + x^2 + x \end{bmatrix}_{-3}^{3} = 60\]
コードの例
f(x) = 3 x^2 + 2 x + 1 #対象の方程式
h(x) = x^3 + x^2 + x #代数で求めた積分の解
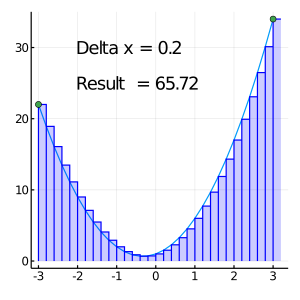
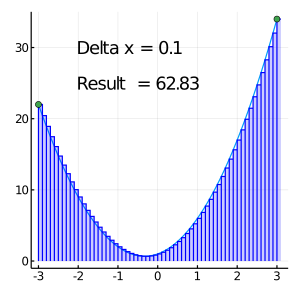
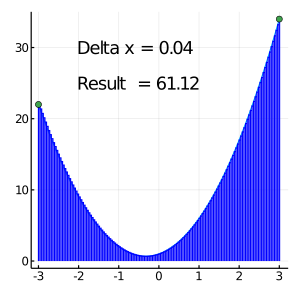
Deltax = 0.2 #xの間隔
x = -3 : Deltax: 3
F = f.(x)
println("Δx = " , Deltax)
println("数値積分結果 = " , sum(F)*Deltax) #本番
println("代数積分結果 = " , h(3 )-h(-3 )) #真の値。比較用
出力:
Δx = 0.2
数値積分結果 = 65.72000000000001
代数積分結果 = 60
*実習1
数値解析で次のコードを完成させて、積分の値を求めてください。
\[ \int_1^3 \sqrt{1 + \cos^2(x) } ~dx \]
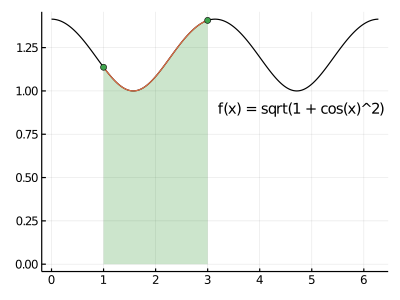
未完成のコード:
f(x) = sqrt(1 + cos(x)^2 )
⋮
出力の例(設計は任意):
課題1の結果 ≈ 2.308973936636286
*実習2:正規分布表の値を求める
標準正規分布の関数こちら:
\[ f(x) = \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \]
その積分は代数で解くことができないので、確率を求めるときは「正規分布表」を用いる。
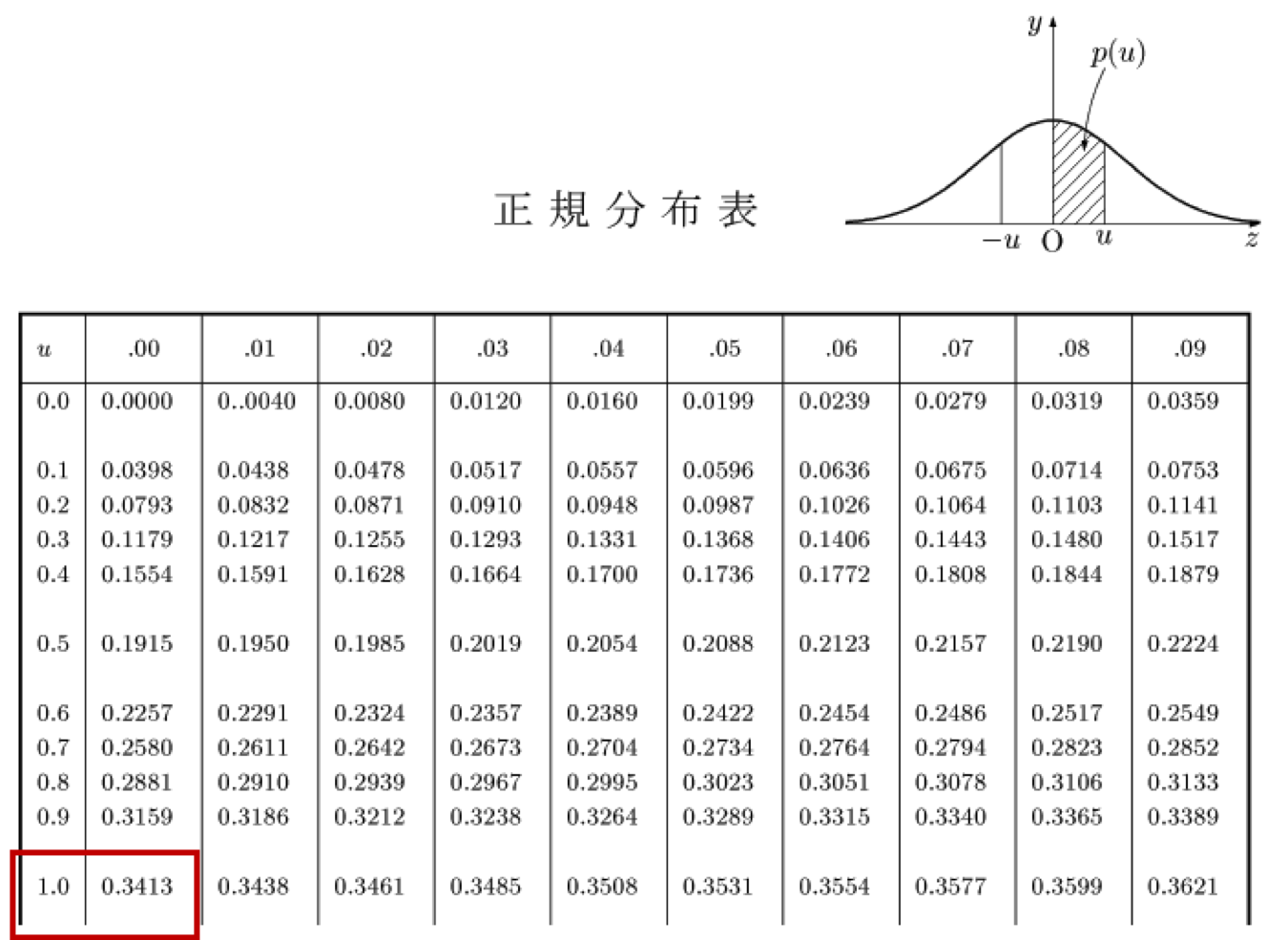
正規分布表により:
\[ \int_0^1 \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) ~dx \approx 0.3413\]
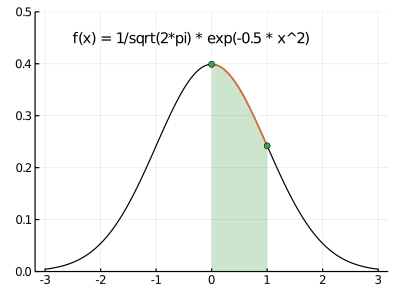
次のコードを完成させて、「正規分布表」に載っている値
f(x) = 1 /sqrt(2 *pi) * exp(-0.5 * x^2 )
⋮
表示の出力スタイルは任意
5. 数値微分
微分の定義
\[ y = f(x) \]
\[ \frac{dy}{dx} = f^{\prime}(x) = \lim_{\Delta x\to0} \frac{f(x + \Delta x)-f(x)}{\Delta x} \]
数値微分,かつΔx が一定の場合:
\[ f^{\prime}(x) \approx \frac{f(x_{i+1}) -f(x_i)}{\Delta x} \]
or
\[ f^{\prime}(x) \approx \frac{f(x_{i}) -f(x_{i-1})}{\Delta x} \]
練習:代数で解ける例で検証
\[ f(x) = x^2 + 2x + 1 \]
\[ f^{\prime}(x) = 2x + 2 \]
コード:
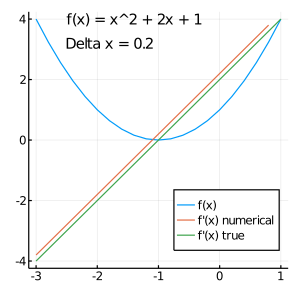
f(x) = x^2 + 2 x + 1
g(x) = 2 *x + 2 #代数で求めた微分の解。比較用
Deltax = 0.2 #この数値を変えてみる。
x = -3 :Deltax:1
F = f.(x)
dfdx = ( F[2 :end] - F[1 :end-1 ] ) /Deltax #本番
plot(size=(300,300 ), legend=:bottomright)
plot!(x, F, label = "f(x)" )
plot!(x[1 :end-1 ], dfdx, label = "f'(x) numerical" )
plot!(x, g.(x), label = "f'(x) true" ) #代数微分。比較用
annotate!(-2.5 , 4 , text("f(x) = x^2 + 2x + 1" , :left, 10 ))
annotate!(-2.5 , 3.2 , text("Delta x = 0.2" , :left, 10 ))
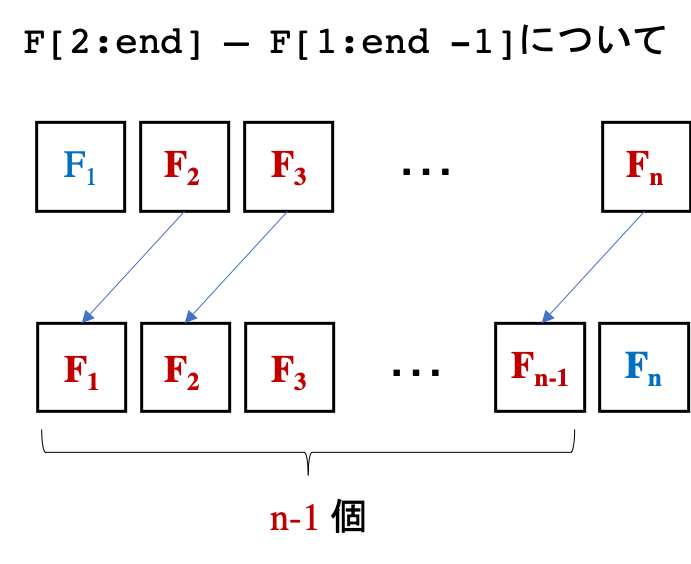
出力:
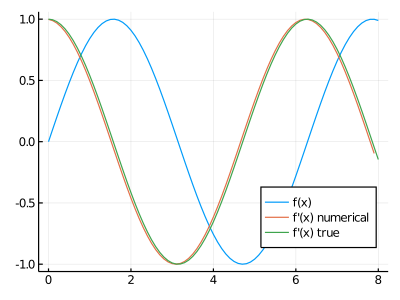
*実習3
数値解析の手法で微分
\[ f(x) = \sin(x) \]
最初は Δx を0.2 にして、誤差強調する。その後はより誤差の低い値にしてください。
6. ニュートン法による方程式の近似解法
• Newton's method. 詳細は こちら
• 最もよく知られた求根アルゴリズムの1つ
概念
微分の定義から始めましょう:
\[ f^{\prime} (x) = \frac{d}{dx} f(x) \]
数値計算の場合:
\[ f^{\prime} (x) = \frac{\Delta f(x)}{\Delta x} \]
\[ \Delta x = \frac{\Delta f(x)}{f^{\prime} (x)} \]
\[ x_{new} - x_{old} = \frac{\Delta f(x_{old})}{f^{\prime} (x_{old})} \]
\[ x_{new} - x_{old} = \frac{f(x_{target})- f(x_{old})}{f^{\prime} (x_{old})} \]
目的は\( f(x_{target}) = 0\)にするので、最終的に下記の式になります:
\[ x_{new} = x_{old} - \frac{f(x_{old})}{f^{\prime} (x_{old})} \]
計算手順(アルゴリズム)
1) f(x) を定義。
2) f'(x) を算出
3) 初期値 x を適当に選出。
4) x = x - f(x)/f'(x) でxの更新を行う。
5) f(x)が0に近つくまで (4)を繰り返す。
根が存在すれば、 f(x) が収束する。
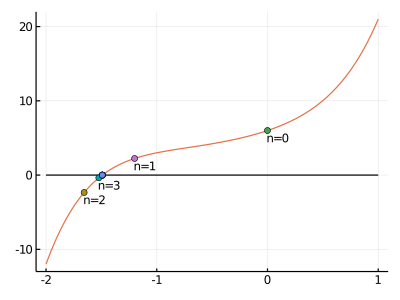
練習:5次元方程式
下記の方程式の近似解を求める。
\[x^5 + 2x^4 + 3x^3 + 4x^2 + 5x + 6 = 0 \]
手作業で、関数の定義と微分を算出:
\[ f(x) = x^5 + 2x^4 + 3x^3 + 4x^2 + 5x + 6\]
\[ f'(x) = 5x^4 + 8x^3 + 9x^2 + 8x + 5 \]
コード
f(x) = x^5 + 2 *x^4 + 3 *x^3 + 4 *x^2 + 5 *x + 6
g(x) = 5 x^4 + 8 x^3 + 9 x^2 + 8 x + 5 #微分
x = 0 #初期値、任意の値。変えてみてください。
println("n = " , 0 , "\tx = " , x, "\tf(x) = " , f(x))
for n in 1:10 #更新回数を10に設定。足りなかったら回数を増やす。
x = x - f(x)/g(x) #ここがメインである。xの更新則
println("n = " , n, "\tx = " , x, "\tf(x) = " , f(x))
end
出力:
n = 0 x = 0 f(x) = 6
n = 1 x = -1.2 f(x) = 2.23488
n = 2 x = -1.655725938009788 f(x) = -2.3427109331385854
n = 3 x = -1.5233077662581676 f(x) = -0.3722464587561678
n = 4 x = -1.493147509509252 f(x) = -0.015276792091255764
n = 5 x = -1.4918005502998353 f(x) = -2.8949045308479526e-5
n = 6 x = -1.4917979881491503 f(x) = -1.0450840193243494e-10
n = 7 x = -1.4917979881399006 f(x) = 8.881784197001252e-16
n = 8 x = -1.4917979881399006 f(x) = 8.881784197001252e-16
n = 9 x = -1.4917979881399006 f(x) = 8.881784197001252e-16
n = 10 x = -1.4917979881399006 f(x) = 8.881784197001252e-16
*実習4
数値解析で下記の方程式の近似解を求める。
\[x^4 + 2x^3 + 3x^2 + 4x - 5 = 0 \]
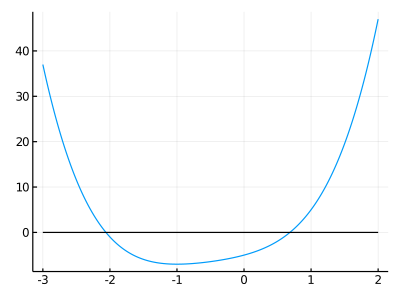
解が2つあります。x の初期値を変えて、両方の値を求めてください。
チャレンジ (提出任意)
時間があったら下記の方程式も試してみる。
\[x^4 + 2x^3 + 3x^2 + 4x + 5 = 0 \]
その結果の原因を考えてみてください。