線形回帰・移動平均・データ解析の実践
1. *事前作業
(1) 実習課題用のフォルダーの作成
各自の
• フォルダー名は任意です。
今回の授業に使う、
VSCode で作業フォルダを開く
VSCode のWeb版のリンクはこちら:https://vscode.dev/
• 各課題につき、
• jlファイルを全て提出してください。
Juliaのターミナで include の方法で、コードを実行してください。
• 重要な出力画面 & グラフは,
• VScode を立ち上げて、
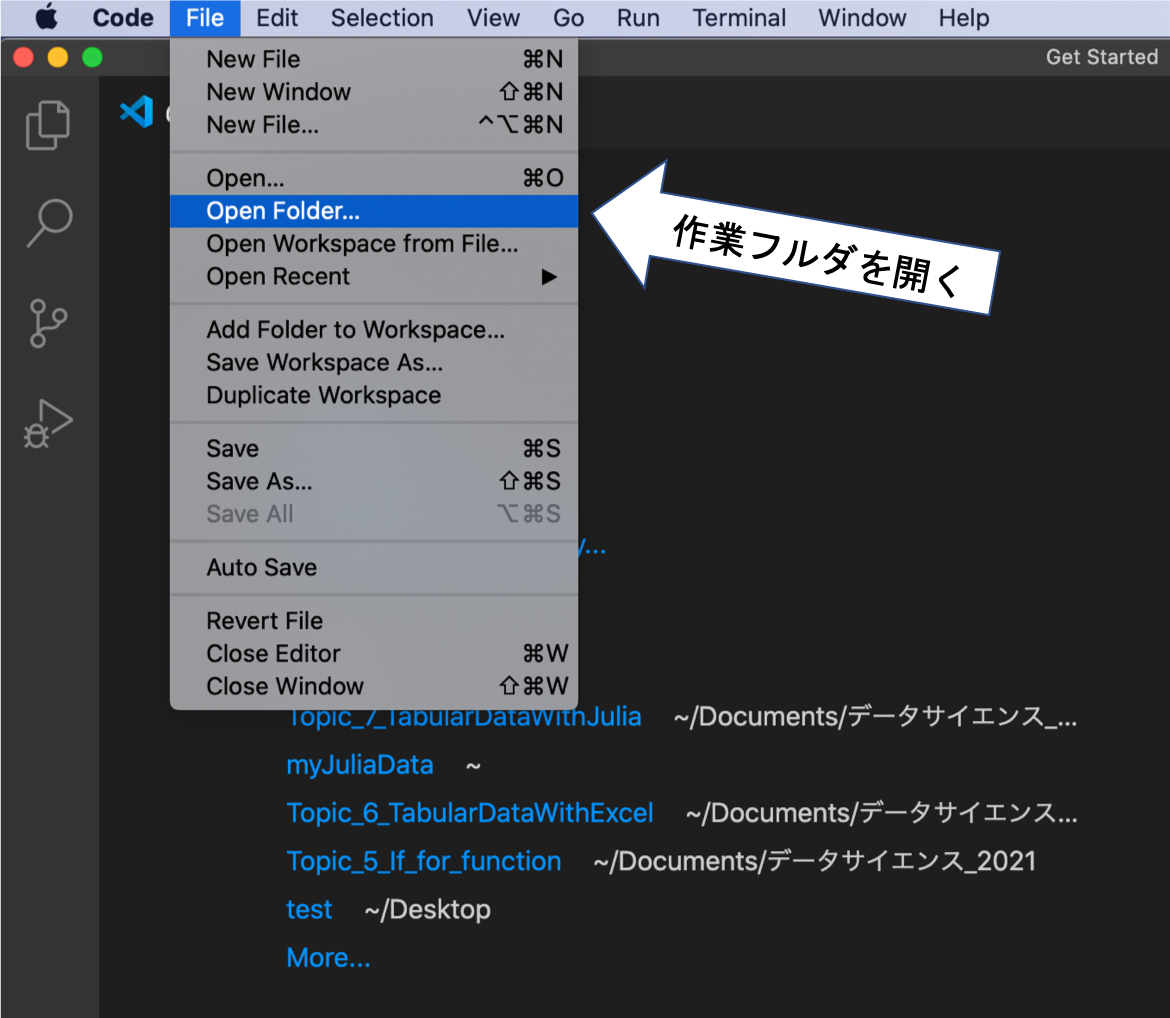
プラグラムのファイルを保存
•
•
cd で作業空間の変更
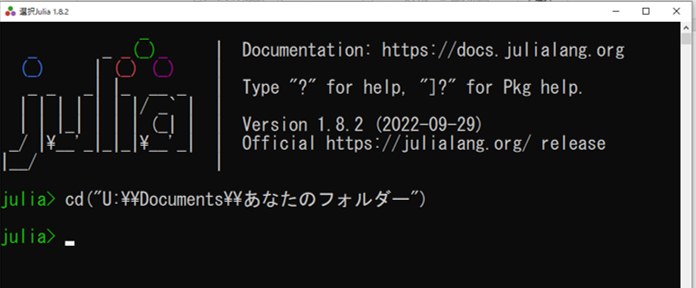
• Julia ターミナル(REPL)を開き、下記のとおりに、
julia> cd("U:\\Documents\\あなたのフォルダー名" )
ターミナルの出力の例:
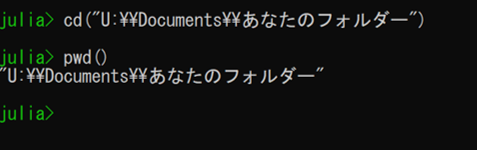
作業空間が確実に変更されたかどうか次のコマンドで確認できる。
julia> pwd()
表示されたフォルダー名が、あなたが作ったものと一致すれば大丈夫です。
例:
include 関数で .jl ファイルを実行する
• Julia端末で
julia> include("あなたのファイル名.jl" )
実行例:
2. レポート課題について:
課題:5問
• 各課題につき、1つのJuliaプログラムファイル(.jl)を使ってください。
• 統計結果及びグラフを1つの Word ファイルにまとめてください。
► 形式は自由ですが、読みやすくようにお願いします。
提出ファイル:
• Word (.docx)
• すべてのJuliaプログラムファイル(.jl)
必要なJulia パケージ
プログラムの冒頭に次のコードを挿入する。
using DataFrames #表データの取り扱い
using CSV #テキストファイルをDataFrameに読み込む
using Plots #グラフの作成
using Statistics #平均値、標本標準偏差、相関係数など
using Random #ランダムの乱数
using LinearAlgebra #線形代数、転置
using Dates #年月日のフォーマット
3. 必要なJulia 関数と復習
mean & std 平均 & 標準偏差
julia> x = 0.4 *randn(10000 ) .+ 5 ; # 標準偏差 0.4, 平均値 5.0 の正規分部乱数列を作成する。
julia> mean(x) #平均値を求める
5.000221046494583
julia> std(x) #標準の偏差を求める
0.40202475952220845
hcat 関数で配列を水平に連結
julia> a = [1,2 ,3 ]
3 -element Array{Int64,1 }:
1
2
3
julia> b = [7,8 ,9 ]
3 -element Array{Int64,1 }:
7
8
9
julia> hcat(a,b)
3×2 Array{Int64,2 }:
1 7
2 8
3 9
4. 今度の課題に使用する csv データ
日本気象庁の過去の気象データ
各地の日平均気温(℃)、平均湿度(%)、平均現地気圧(hPa)、降水量の合計(mm)
期間:2017年1月1日〜2022年12月31日
次のファイルを「右クリック」、「名前を付けて保存」で作業フォルダーに保存してください。
•
► ファイル:weather_kofu_2017-2022.csv
•
► ファイル:weather_naha_2017-2022.csv
•
► ファイル:weather_nagasaki_2017-2022.csv
•
► ファイル:weather_sapporo_2017-2022.csv
•
► ファイル:weather_yokohama_2017-2022.csv
データの確認
コピーペーで、次のコードを実行して、データの読み込みを確認する。
#データの読み込む
KF = CSV.read("weather_kofu_2017-2022.csv" ,DataFrame, comment = "#" )
NH = CSV.read("weather_naha_2017-2022.csv" ,DataFrame, comment = "#" )
SP = CSV.read("weather_sapporo_2017-2022.csv" ,DataFrame, comment = "#" )
YK = CSV.read("weather_yokohama_2017-2022.csv" ,DataFrame, comment = "#" )
#データの確認
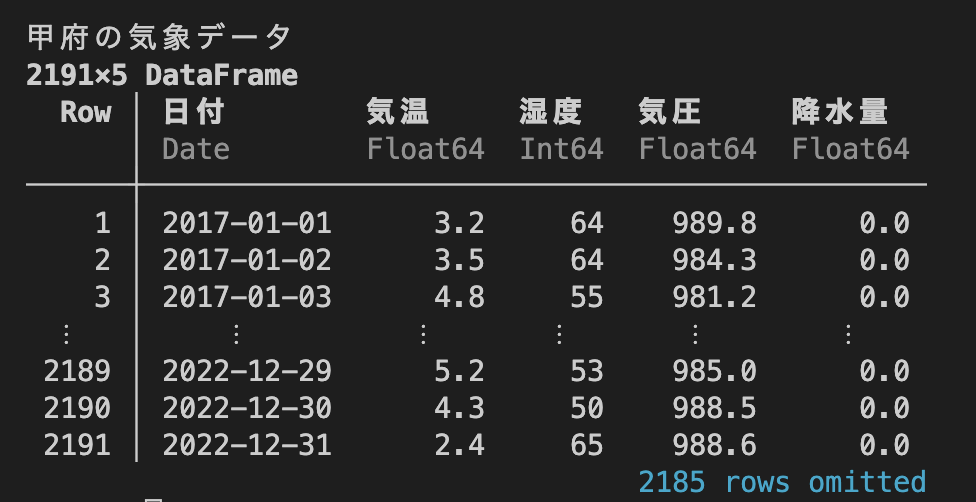
println("甲府の気象データ" )
show(KF)
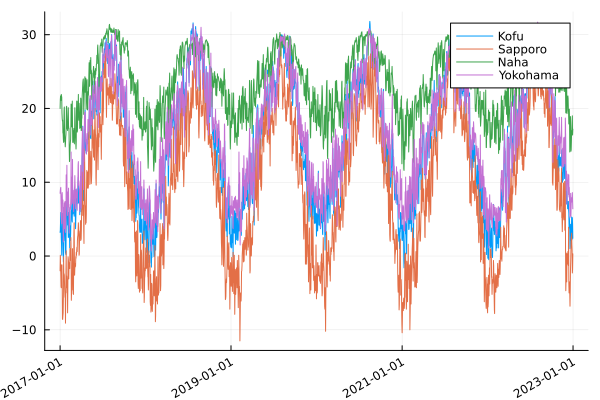
#6年間 日平均気温のグラフ
plot(KF.日付, KF.気温, xrotation = 30 , label = "Kofu" )
plot!(SP.日付, SP.気温, label = "Sapporo" )
plot!(NH.日付, NH.気温, label = "Naha" )
plot!(YK.日付, YK.気温, label = "Yokohama" )
出力:
5. *課題1:甲府と横浜の気圧
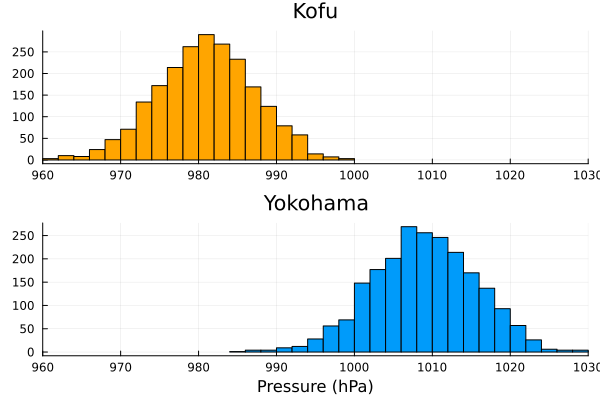
甲府と横浜の気圧データを分析し、次の出力とヒストグラムを作成するためのJulia コードを書いてください。
• 色とスタイルは任意です
• 横軸の範囲を統一する
• ヒストグラムに関する参考資料:Topic 11
• グラフ範囲など、グラフの一般参考資料:「Julia Plotについて」
出力
甲府の平均気圧(hPa) = 980.8499771793701
標準偏差 = 6.203819618054691
横浜の平均気圧(hPa) = 1008.8508443633045
標準偏差 = 6.629641337500394
6. 回帰分析 Regression
• 元々は生物学的現象を表す方法。
• 英語 regression の直訳は「後退」という意味で、ばらついたデータが「平均への回帰」という現象を表す。
• 現在では「データのモデルを当てはめる」のことを表す。
例:データYとXをf 関数で表す。
\[\mathbf{Y} = f(\mathbf{X}) \]
図1:15名の学生の身長(cm)と体重のデータ (相関係数 = 0.8)
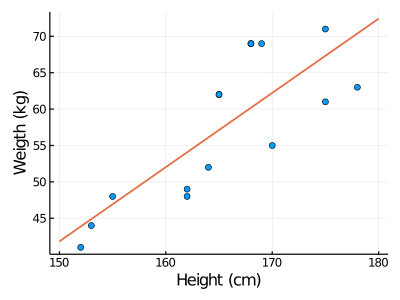
関連情報(wikipedia):
7. 最小二乗法の一般公式を線形代数で表す
\[y = f(x) + \epsilon\]
誤差 ϵ の二乗の和を最小にする。
線形回帰の場合:
\[\begin{aligned}y_1 &= x_{11}b_1 + x_{12}b_2 + \cdots + x_{1m}b_m + \epsilon_1 \\y_2 &= x_{21}b_1 + x_{21}b_2 + \cdots + x_{2m}b_m + \epsilon_2 \\\vdots\\y_n &= x_{n1}b_1 + x_{n1}b_2 + \cdots + x_{nm}b_m + \epsilon_n \\\end{aligned}\]
行列で表すと:
\[\begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix} = \begin{pmatrix}x_{11} & x_{12} &\cdots &x_{1m} \\x_{21} & x_{22} &\cdots &x_{2m} \\\vdots & \vdots &\cdots &\vdots \\x_{n1} & x_{n2} &\cdots &x_{nm} \\\end{pmatrix}\begin{pmatrix}b_1\\b_2\\\vdots\\b_m\end{pmatrix} + \begin{pmatrix}\epsilon_1\\\epsilon_2\\\vdots\\\epsilon_n\end{pmatrix}\]
コンパクで表すと:
\[\mathbf{Y} = \mathbf{X} \mathbf{b} + \mathbf{e}\]
誤差を最小限するには
\[\begin{aligned}\mathbf{b} &= (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\\\end{aligned}\]
証明
誤差のベクトル:\[\mathbf{e} = \mathbf{Y} - \mathbf{X}\mathbf{b}\]行列の微分:\[\frac{\partial \mathbf{e}}{\partial \mathbf{b}} = -\mathbf{X}\]誤差の二乗の和とその微分\[S = \epsilon_1^2 + \epsilon_2^2 + \cdots \epsilon_n^2 = \mathbf{e}^T \mathbf{e}\]\[\begin{aligned}\Delta S &= \frac{\partial S}{\partial \epsilon_1} \Delta \epsilon_1 + \cdots + \frac{\partial S}{\partial \epsilon_n} \Delta \epsilon_n\\\\&= \begin{pmatrix} 2\epsilon_1 &2\epsilon_2 &\cdots &2\epsilon_n\end{pmatrix}\begin{pmatrix}\Delta \epsilon_1 \\\Delta \epsilon_2\\\vdots\\\Delta \epsilon_n\end{pmatrix}\end{aligned}\]整理したら:\[\frac{\partial S}{\partial \mathbf{e}} = \frac{\Delta S}{\Delta \mathbf{e}} = 2\mathbf{e}^T\]誤差の二乗の和 S を最小にすには:\[\frac{\partial S}{\partial \mathbf{b}} = \mathbf{0}\]上記の微分を求めるために、次の関係を利用する。\[\frac{\partial S}{\partial \mathbf{b}} = \frac{\partial S}{\partial \mathbf{e}} ~ \frac{\partial e}{\partial \mathbf{b}}\]\[\begin{aligned}\frac{\partial S}{\partial \mathbf{b}} &= - 2\mathbf{e}^T \mathbf{X}\\&= -2(\mathbf{Y} - \mathbf{X}\mathbf{b})^T \mathbf{X}\end{aligned}\]では、dS/db = 0 にする。\[\begin{aligned}(\mathbf{Y}^T - \mathbf{b}^T\mathbf{X}^T) \mathbf{X} = \mathbf{0}\\\mathbf{Y}^T\mathbf{X} - \mathbf{b}^T\mathbf{X}^T \mathbf{X} = \mathbf{0}\end{aligned}\]整理したら:\[\begin{aligned}\mathbf{b}^T\mathbf{X}^T \mathbf{X} &= \mathbf{Y}^T\mathbf{X}\\\end{aligned}\]両側を転置したら:\[\begin{aligned}\mathbf{X}^T \mathbf{X}\mathbf{b} &= \mathbf{X}^T\mathbf{Y}\\\end{aligned}\]最後は:\[\begin{aligned}\mathbf{b} &= (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\\\end{aligned}\]
8. 最小二乗法: 乱数関数を用いて検証
主な式はこちら:
b = inv(transpose(X)*X) * transpose(X) * Y
!練習:モデル y = b1*x + b2
下記のモデルを使います:
\[\begin{aligned}y_1 &= x_1 b_1 + b_2\\\vdots &= \vdots\\y_n &= x_n b_1 + b_2\end{aligned}\]
行例で表す:
\[\begin{aligned}\mathbf{Y} &= \mathbf{X}\mathbf{b}\\\\&=\begin{pmatrix}x_1 & 1\\\vdots & \vdots\\x_n &1 \end{pmatrix}\begin{pmatrix}b_1 \\b_2 \end{pmatrix}\end{aligned}\]
乱数を用いて検証する:
# モデル: y = a1*x + a2
a1 = 2 # 真値: a1 = 2, a2=4
a2 = 4
x = Array(0:0 .1:5 )
Noise = randn(length(x)) #randn は 標準正規分布の乱数を作成
y = a1*x .+ a2 .+ Noise
#散布図を作成
scatter(x, y, legend = false, size = (400,300 ))
#これが本番。まずはデータを行列の形にする
X = hcat(x, ones(length(x)))
Y = y
#主な演算式はこちら
b = inv(transpose(X)*X) * transpose(X) * Y
println("モデル: y = " ,a1,"x + " ,a2)
println("最小二乗法で求めた線形回帰係数の結果:" )
println("b1 = " , b[1 ])
println("b2 = " , b[2 ])
# b1:傾き、 b2:y 切片
# 算出した b1 と b2 で直線を作成して、グラフに追加する
y2 = x*b[1 ] .+ b[2 ]
plot!(x, y2, linewidth = 2 )
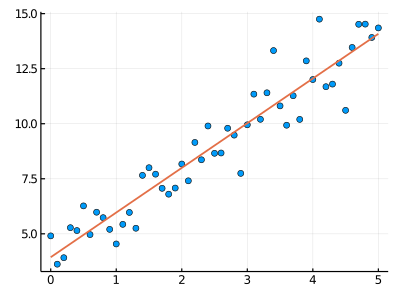
出力:
モデル: y = 2x + 4
最小二乗法で求めた線形回帰係数の結果:
b1 = 2.029151596748406
b2 = 3.937559023888329
9. *課題2:甲府と札幌の気温
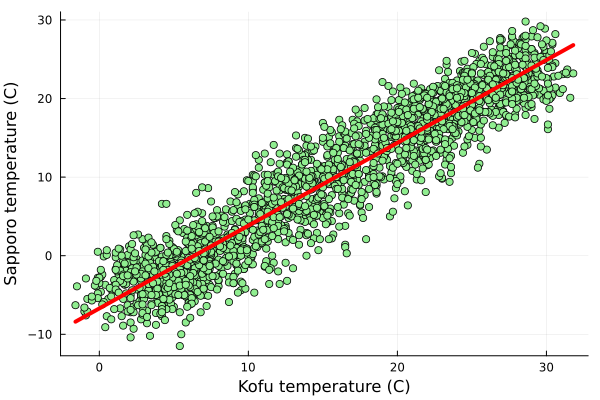
次のコードを完成させて、甲府と札幌の気温回帰直線・近似直線を作成する。
• 最小二乗法の練習例を参考にする。
• 色をグラフのサイズは任意です。
#最小二乗法で甲府の日平均気温と札幌の日平均気温
#の近似直線を作成する
x = KF.気温
y = SP.気温
scatter(x,y, legend = false,
xlabel = "Kofu temperature (C)" ,
ylabel = "Sapporo temperature (C)" , c=:lightgreen)
#このコードを完成させ。
10. *課題3:DataFrameを使ってデータを抽出
表式データ から条件付けで必要なデータだけ抽出する。
方法は 括弧[ ]の中に条件を記入する。
まずは次のコードを書き込んでください。このコードは次のことを実施する。
► 元データから 2022年のデータだけ抽出する。
► 2022年のデータから雨の日だけ抽出する。
► 雨の日を大きい緑点で表す。
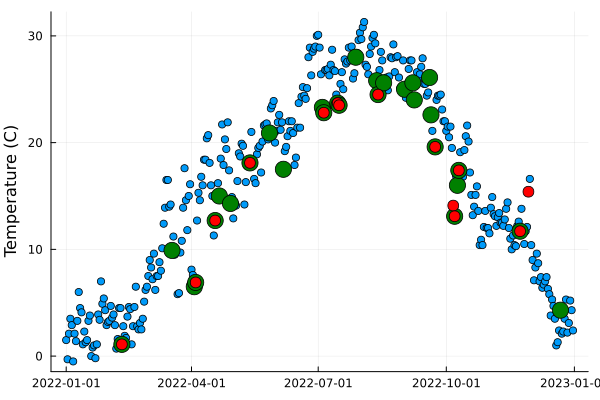
#甲府 2022年以降の気温
x = KF.日付[KF.日付 .>= Date(2022 )]
y = KF.気温[KF.日付 .>= Date(2022 )]
scatter(x,y, legend = false, ylabel = "Temperature (C)" )
#甲府 2022年以降 かつ 降水量が 10 を超える データ
x2 = KF.日付[(KF.日付 .>= Date(2022 )) .& (KF.降水量 .> 10 )]
y2 = KF.気温[(KF.日付 .>= Date(2022 )) .& (KF.降水量 .> 10 )]
#マーカサイズで雨の日を強調する。
scatter!(x2, y2, color=:green ,marker = 9 )
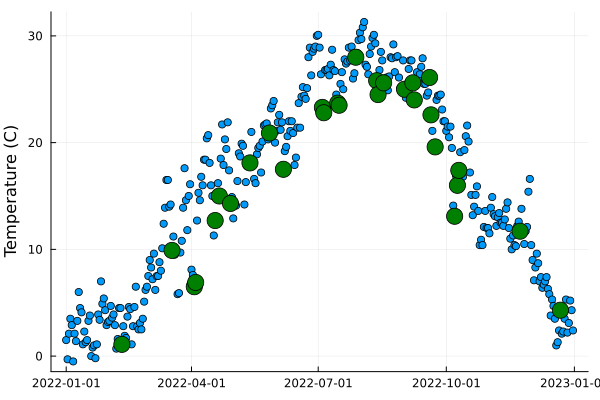
上記のコードに次の分析項目を追加する:
• 甲府 2022年以降 かつ 湿度が 90 を超えるデータポイントを抽出する。
• そのデータを赤いマーカーでグラフに追加する。
グラフ:
11. *課題4&課題5:自由課題
自分なりの方法で気象データの統計解析を行う
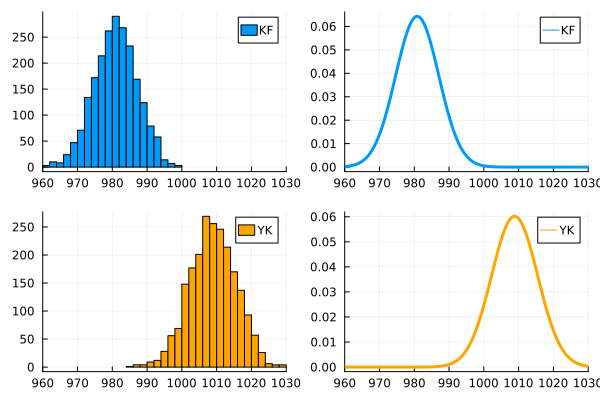
例:甲府と横浜の気圧正規分布
正規分布の参照:Topic 12
甲府気圧平均値 = 980.8499771793701
甲府気圧偏差値 = 6.203819618054691
横浜気圧平均値 = 1008.8508443633045
横浜気圧偏差値 = 6.629641337500394
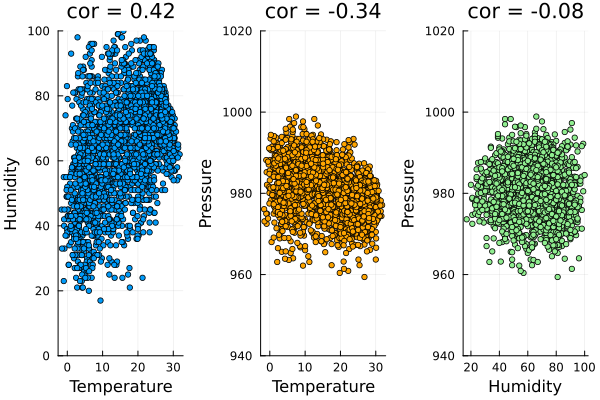
例:気温、湿度、気圧の相関
正規分布の参照:Topic 11
気温と湿度の相関係数 = 0.4234173678069623
気温と気圧の相関係数 = -0.3364130552816557
湿度と気圧の相関係数 = -0.07720466847037719
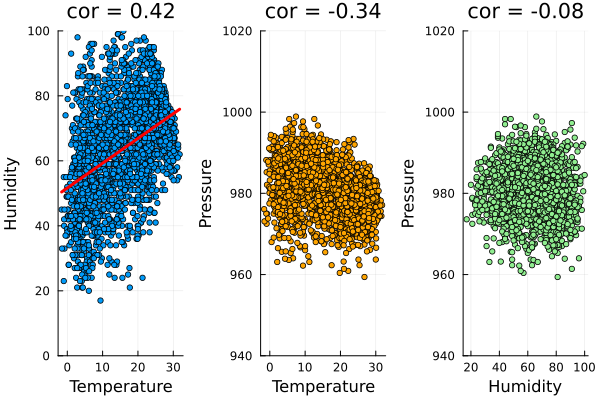
例:気温、湿度の回帰直線
12. 他の例:単純移動平均 Simple Moving Average
• データを平滑化する手法の1つ
周りのデータ点を使って平均値を求める
次は3点の単純移動平均の例を示す
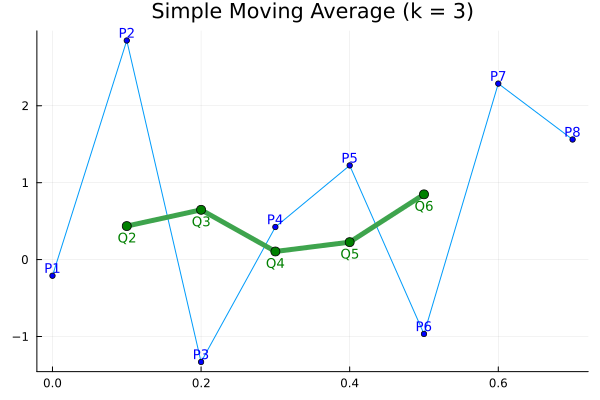
\[Q_2 = (P_1 + P_2 + P_3)/3\]
\[Q_3 = (P_2 + P_3 + P_4)/3\]
\[Q_i = (P_{i-1}+ P_{i} + P_{i+1})/3\]
Juliaで単純移動平均を行う:
# Simple Moving Average 単純移動平均
# コピーペーで次の自作関数を自分のコードに貼り付ける
# 使い方:
# (xs, ys) = SMA(x, y, k)
# x と y は入力データ
# k は平均演算に使う数.(奇数)
# xs と ys は平滑されたデータ
function SMA(x, y, k) #重要:k は奇数
N = length(y)
result = zeros(N - k)
for n=1 :k
result += y[n:N-k+n-1 ]
end
result = result/k
return (x[floor(Int, k/2 + 1 ):end-floor(Int, k/2 )-1 ], result)
end
# ここからはテスト用のコードです
x = -4:0 .1:4
y = x.^2 + randn(length(x)) #雑音のあるデータ
# 自作の単純移動平均関数 SMA で平滑化を行う
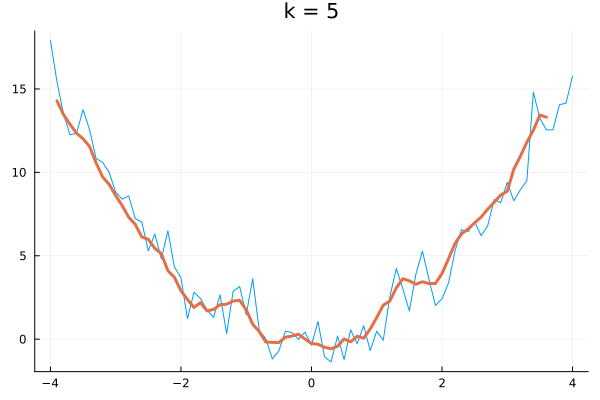
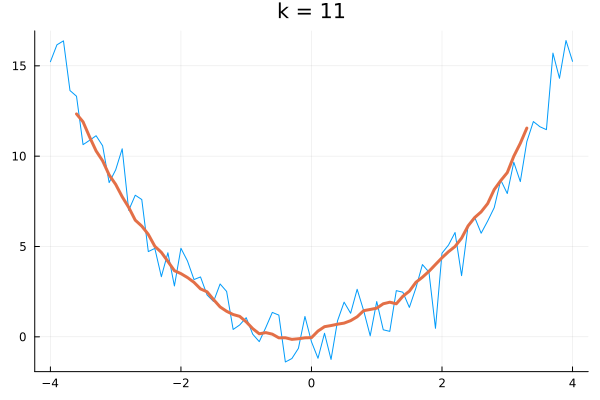
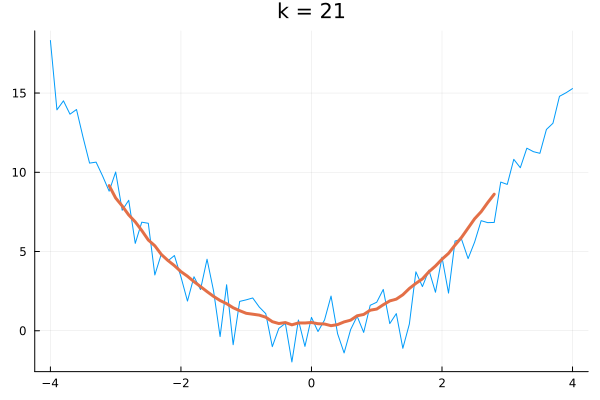
k = 5 # 平均の計算に使うデータ数
(xs, ys) = SMA(x, y,k)
plot(x,y, legend = false)
plot!(xs, ys, w=3 , title = "k = 5" )
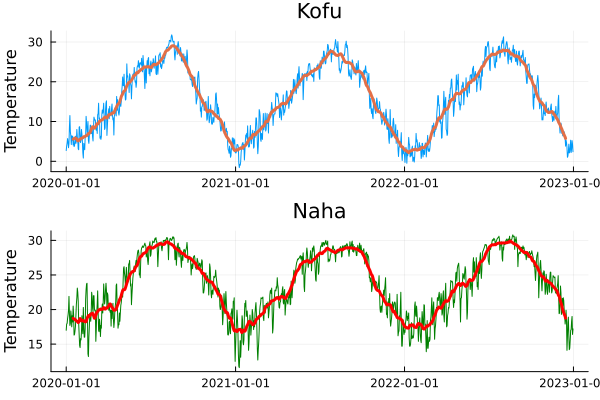
例:甲府と那覇の年間平均気温(2020~2022)
甲府の気温(3年間の平均)= 15.799635036496348
標準偏差 = 8.475075455491181
那覇の気温(3年間の平均)= 23.709489051094888
標準偏差 = 4.550363657891322
13. 他の例:ソーティング sort 関数
sort 関数で配列、データの内容を並べ替えます
例:ソーティング(昇順)
julia> 寒い日 = sort(KF, :気温)

julia> 寒い日[1 , :気温] #一番寒い日の日平均気温 [C]
-1.6
julia> 寒い日[1 , :日付] #一番寒い日の日付
2021-01 -09
julia> 寒い日[2 , :日付] #2番寒い日の日付
2018-01 -26
例:逆順のソーティング(降順)
julia> 雨の日 = sort(KF, :降水量, rev = true)

julia> 雨の日[1 , :降水量] #一番雨の多い日の降水量 [mm]
169.0
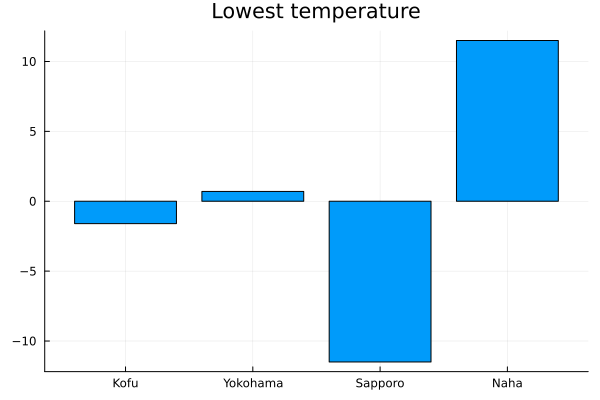
例:各都市の最低日平均気温
• bar は棒グラフです。使い方は plot, scatter と同様です。
julia> 都市 = ["Kofu" , "Yokohama" , "Sapporo" , "Naha" ];
julia> 最低気温 = [sort(KF,:気温)[1 ,:気温],
sort(YK,:気温)[1 ,:気温],
sort(SP,:気温)[1 ,:気温],
sort(NH,:気温)[1 ,:気温]];
julia> bar(都市, 最低気温, title = "Lowest temperature" , legend = false)