線形回帰 & ビグデータ
今回の実習課題について:
• 課題:5問
• 提出ファイル1(Word .docx)
► 説明付きで、作成したコードの内容、出力画面とグラフのまとめ。
► 形式は自由ですが、読みやすくようにお願いします。
次の Julia パケージを使います:
► DataFrames 表データの取り扱い
► CSV テキストファイルをDataFrameに読み込む
► Plots グラフの作成
► Statistics 平均値、標本標準偏差、相関係数など
► Random ランダムの乱数
► LinearAlgebra 線形代数、転置
► Dates 年月日のフォーマット
各自のプログラムの最初の所に下記のコードを挿入する。
using DataFrames
using CSV
using Plots
using Statistics
using Random
using LinearAlgebra
using Dates
1. 線形代数の復習と必要なJulia 関数
ベクトルの内積
\[\begin{aligned}\mathbf{a} \bullet \mathbf{b} &= a_1 b_1 + a_2 b_2 + \cdots + a_n b_n\\\\ &= \begin{pmatrix} a_1 &a_2 &\cdots &a_n\end{pmatrix}\begin{pmatrix} b_1\\b_2\\ \vdots \\b_n\end{pmatrix}\\\\ &= \mathbf{a}^T \mathbf{b}\\\\ &= \mathbf{b}^T \mathbf{a}\\\\\end{aligned}\]
二乗の和を線形代数で表す
\[ \mathbf{a}^T \mathbf{a} = a_1^2 + a_2^2 + \cdots + a_n^2\]
転置の演算
\[ (\mathbf{a} + \mathbf{b})^T = \mathbf{a}^T + \mathbf{b}^T \]
\[ (\mathbf{a}\mathbf{b})^T = \mathbf{b}^T \mathbf{a}^T \]
hcat 関数で配列を水平に連結
julia> a = [1,2 ,3 ]
3 -element Array{Int64,1 }:
1
2
3
julia> b = [7,8 ,9 ]
3 -element Array{Int64,1 }:
7
8
9
julia> hcat(a,b)
3×2 Array{Int64,2 }:
1 7
2 8
3 9
sort 関数でソーティングをする
julia> a = rand(1:9 , 10 )
10 -element Array{Int64,1 }:
7
5
5
8
6
6
3
4
7
1
julia> sort(a)
10 -element Array{Int64,1 }:
1
3
4
5
5
6
6
7
7
8
julia> sort(a, rev = true)
10 -element Array{Int64,1 }:
8
7
7
6
6
5
5
4
3
1
2. 回帰分析 Regression
• 元々は生物学的現象を表す方法。
• 英語 regression の直訳は「後退」という意味で、ばらついたデータが「平均への回帰」という現象を表す。
• 現在では「データのモデルを当てはめる」のことを表す。
例:データYとXをf 関数で表す。
\[\mathbf{Y} = f(\mathbf{X}) \]
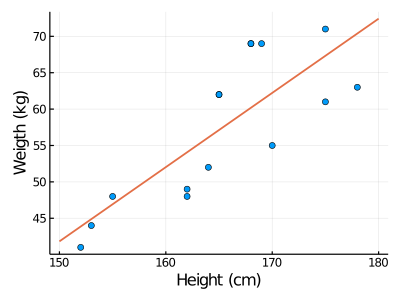
図1:15名の学生の身長(cm)と体重のデータ (相関係数 = 0.8)
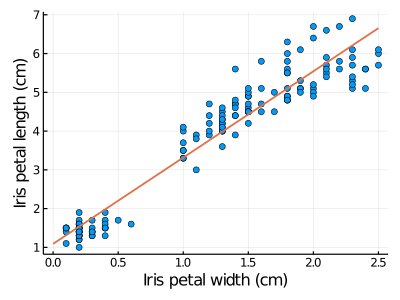
図2:花 Iris の花弁の幅 (petal width) と 長さ (petal length)のデータ (相関係数 = 0.96)
関連情報(wikipedia):
3. 最小二乗法の公式:線形代数で導く
\[y = f(x) + \epsilon\]
誤差 ϵ の二乗の和を最小にする。
線形回帰の場合:
\[\begin{aligned}y_1 &= x_{11}b_1 + x_{12}b_2 + \cdots + x_{1m}b_m + \epsilon_1 \\y_2 &= x_{21}b_1 + x_{21}b_2 + \cdots + x_{2m}b_m + \epsilon_2 \\\vdots\\y_n &= x_{n1}b_1 + x_{n1}b_2 + \cdots + x_{nm}b_m + \epsilon_n \\\end{aligned}\]
行列で表すと:
\[\begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix} = \begin{pmatrix}x_{11} & x_{12} &\cdots &x_{1m} \\x_{21} & x_{22} &\cdots &x_{2m} \\\vdots & \vdots &\cdots &\vdots \\x_{n1} & x_{n2} &\cdots &x_{nm} \\\end{pmatrix}\begin{pmatrix}b_1\\b_2\\\vdots\\b_m\end{pmatrix} + \begin{pmatrix}\epsilon_1\\\epsilon_2\\\vdots\\\epsilon_n\end{pmatrix}\]
コンパクで表すと:
\[\mathbf{Y} = \mathbf{X} \mathbf{b} + \mathbf{e}\]
誤差のベクトル:
\[\mathbf{e} = \mathbf{Y} - \mathbf{X}\mathbf{b}\]
行列の微分:
\[\frac{\partial \mathbf{e}}{\partial \mathbf{b}} = -\mathbf{X}\]
誤差の二乗の和とその微分
\[S = \epsilon_1^2 + \epsilon_2^2 + \cdots \epsilon_n^2 = \mathbf{e}^T \mathbf{e}\]
\[\begin{aligned}\Delta S &= \frac{\partial S}{\partial \epsilon_1} \Delta \epsilon_1 + \cdots + \frac{\partial S}{\partial \epsilon_n} \Delta \epsilon_n\\\\&= \begin{pmatrix} 2\epsilon_1 &2\epsilon_2 &\cdots &2\epsilon_n\end{pmatrix}\begin{pmatrix}\Delta \epsilon_1 \\\Delta \epsilon_2\\\vdots\\\Delta \epsilon_n\end{pmatrix}\end{aligned}\]
整理したら:
\[\frac{\partial S}{\partial \mathbf{e}} = \frac{\Delta S}{\Delta \mathbf{e}} = 2\mathbf{e}^T\]
誤差の二乗の和 S を最小にすには:
\[\frac{\partial S}{\partial \mathbf{b}} = \mathbf{0}\]
上記の微分を求めるために、次の関係を利用する。
\[\frac{\partial S}{\partial \mathbf{b}} = \frac{\partial S}{\partial \mathbf{e}} ~ \frac{\partial e}{\partial \mathbf{b}}\]
\[\begin{aligned}\frac{\partial S}{\partial \mathbf{b}} &= - 2\mathbf{e}^T \mathbf{X}\\&= -2(\mathbf{Y} - \mathbf{X}\mathbf{b})^T \mathbf{X}\end{aligned}\]
では、dS/db = 0 にする。
\[\begin{aligned}(\mathbf{Y}^T - \mathbf{b}^T\mathbf{X}^T) \mathbf{X} = \mathbf{0}\\\mathbf{Y}^T\mathbf{X} - \mathbf{b}^T\mathbf{X}^T \mathbf{X} = \mathbf{0}\end{aligned}\]
整理したら:
\[\begin{aligned}\mathbf{b}^T\mathbf{X}^T \mathbf{X} &= \mathbf{Y}^T\mathbf{X}\\\end{aligned}\]
両側を転置したら:
\[\begin{aligned}\mathbf{X}^T \mathbf{X}\mathbf{b} &= \mathbf{X}^T\mathbf{Y}\\\end{aligned}\]
最後は:
\[\begin{aligned}\mathbf{b} &= (\mathbf{X}^T \mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}\\\end{aligned}\]
4. 最小二乗法: 乱数関数を用いて検証
主な式はこちら:
b = inv(transpose(X)*X) * transpose(X) * Y
練習:モデル y = b1*x + b2
下記のモデルを使います:
\[\begin{aligned}y_1 &= x_1 b_1 + b_2\\\vdots &= \vdots\\y_n &= x_n b_1 + b_2\end{aligned}\]
行例で表す:
\[\begin{aligned}\mathbf{Y} &= \mathbf{X}\mathbf{b}\\\\&=\begin{pmatrix}x_1 & 1\\\vdots & \vdots\\x_n &1 \end{pmatrix}\begin{pmatrix}b_1 \\b_2 \end{pmatrix}\end{aligned}\]
乱数を用いて検証する:
# モデル: y = a1*x + a2
a = [2 , 4 ] # 真値: a1 = 2, a2=4
x = Array(0:0 .1:5 )
N = length(x)
Noise = randn(N) #ノイズ:正規分布乱数
#行列の形にする
X = hcat(x, ones(N))
Y = X*a .+ Noise
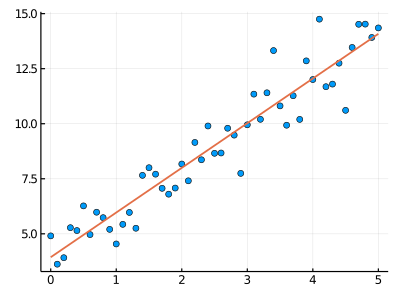
scatter(x, Y, legend = false, size = (400,300 ))
##最小二乗法:
b = inv(transpose(X)*X) * transpose(X) * Y
println("モデル: y = " ,a[1 ],"x + " ,a[2 ])
println("最小二乗法で求めた線形回帰係数の結果:" )
println("b1 = " , b[1 ])
println("b2 = " , b[2 ])
Y2 = X*b
plot!(x, Y2, linewidth = 2 )
出力:
モデル: y = 2x + 4
最小二乗法で求めた線形回帰係数の結果:
b1 = 2.029151596748406
b2 = 3.937559023888329
*実習課題:モデル y = b1*x^2 + b2*x + b3
下記のモデルを使います:
\[\begin{aligned}y_1 &= x_1^2 b_1 + x_1 b_2 + b_3\\\vdots &= \vdots\\y_n &= x_n^2 b_1 + x_1 b_2 + b_3\end{aligned}\]
\[\begin{aligned}\mathbf{Y} &= \mathbf{X}\mathbf{b}\\\\&=\begin{pmatrix}x_1^2 & x_1 & 1\\\vdots & \vdots\\x_n^2 &x_n &1 \end{pmatrix}\begin{pmatrix}b_1 \\b_2\\b_3 \end{pmatrix}\end{aligned}\]
乱数を用いて検証する:
# モデル: y = a1*x^2 + a2*x + a3
a = [2 , 4 , 2 ] #値を変えてみる
x = Array(-3:0 .1:2 )
N = length(x)
Noise = randn(N) #randn は -inf 〜 0〜 +infの乱数を作成
#行列の形にする
X = hcat(x.^2 , x, ones(N))
Y = X*a .+ Noise
scatter(x, Y, legend = false, size = (400,300 ))
#最小二乗法:
b = inv(transpose(X)*X) * transpose(X) * Y
println("モデル: y = " ,a[1 ],"x^2 + " ,a[2 ],"x + " , a[3 ])
println("最小二乗法で求めた線形回帰係数の結果:" )
println("b1 = " , b[1 ])
println("b2 = " , b[2 ])
println("b3 = " , b[3 ])
Y2 = X*b
plot!(x, Y2, linewidth = 2 )
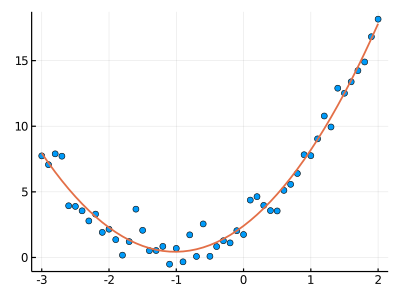
出力:
デル: y = 2x^2 + 4x + 2
最小二乗法で求めた線形回帰係数の結果:
b1 = 1.9094574006719474
b2 = 3.8823305012426026
b3 = 2.4072598480843497
5. 最小二乗法: データを用いて実践(課題)
*実習課題2:十五人の学生の体重と身長の関係
次のコードを完成させる、最小二乗法を用いた回帰曲線を作成する。
身長 = [178 , 165 , 168 , 152 , 175 ,
175 , 165 , 162 , 164 , 170 ,
169 , 155 , 153 , 162 , 168 ]
体重 = [63 , 62 , 69 , 41 , 71 ,
61 , 62 , 48 , 52 , 55 ,
69 , 48 , 44 , 49 , 69 ]
Y = 体重
X = hcat(身長, ones(length(体重)))
scatter(身長, 体重,
legend = false,
xlabel = "Height (cm)" ,
ylabel = "Weigth (kg)" ,
size = (400,300 ))
#また未完成です
❓
出力:
身長と体重の相関係数は:0.7967368727051103
求めた線形回帰係数 b:[1.0200559701493237, -111.18392412936413]
グラフ:

*実習課題3:花 Iris の花弁
• 目的:花 Iris の花弁の幅と長さの関係の線形モデルを立てる。
• データファイル:iris.txt
• DataFrameの使い方について、第11回の授業資料を参照してください。
次のコードを完成させる、最小二乗法を用いた回帰曲線を作成する。
A=CSV.read("iris.txt" , DataFrame)
show(A)
xx = A.petal_width
Y = A.petal_length
X = hcat(xx, ones(length(xx)))
#また未完成です
❓
出力:
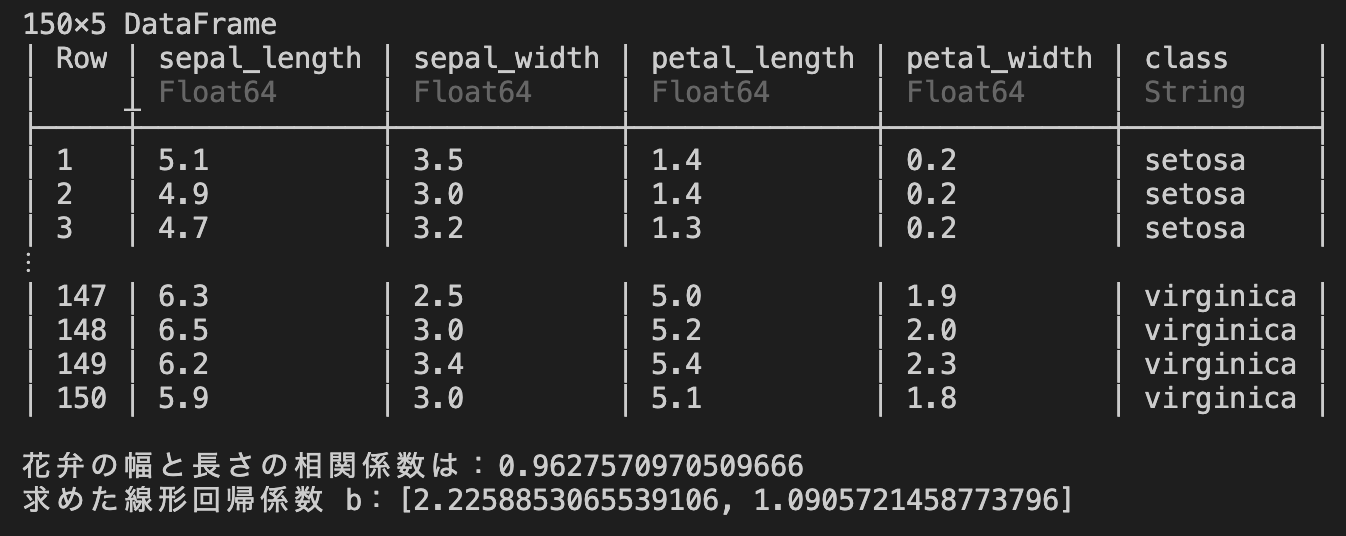
グラフ:

6. ビッグデータ & Missing データ
Big data ビッグデータ

• とても「大きい」データ
• ICT企業さんが考えた定義:従来の統計ソフトウエアで処理できないデータ
Missing データについて
• 現実のデータベースに「未入力」、「未知」なデータだ入っている。
• Julia では、そういうデータを「Mising」というデータの型で扱っている。
julia> a = [1 , 2 , missing]
3 -element Array{Union{Missing, Int64},1 }:
1
2
missing
julia> a + a
3 -element Array{Union{Missing, Int64},1 }:
2
4
missing
julia> a*transpose(a)
3×3 Array{Union{Missing, Int64},2 }:
1 2 missing
2 4 missing
missing missing missing
julia> transpose(a)*a
missing
練習:DataFrame:Missingが入っている行を排除する
dropmissing(表データ) を使って missing のある行をdropする。
練習 例1:
julia> a = [1 , 2 , 3 , 4 ]
4 -element Vector{Int64}:
1
2
3
4
julia> b = [9 , missing, 7 , 6 ]
4 -element Vector{Union{Missing, Int64}}:
9
missing
7
6
julia> df = DataFrame(x = a, y = b)
4×2 DataFrame
Row │ x y
│ Int64 Int64?
─────┼────────────────
1 │ 1 9
2 │ 2 missing
3 │ 3 7
4 │ 4 6
julia> dropmissing(df)
3×2 DataFrame
Row │ x y
│ Int64 Int64
─────┼──────────────
1 │ 1 9
2 │ 3 7
3 │ 4 6
練習 例2:
julia> c = [missing, missing, missing, missing]
4 -element Vector{Missing}:
missing
missing
missing
missing
julia> dg = DataFrame(x = a, y = b, z = c)
4×3 DataFrame
Row │ x y z
│ Int64 Int64? Missing
─────┼─────────────────────────
1 │ 1 9 missing
2 │ 2 missing missing
3 │ 3 7 missing
4 │ 4 6 missing
julia> dropmissing(dg) # missingが入ったらデータを全部排除する
0×3 DataFrame
julia> dropmissing(dg, :y) #y列に missingがあったら排除する
3×3 DataFrame
Row │ x y z
│ Int64 Int64 Missing
─────┼───────────────────────
1 │ 1 9 missing
2 │ 3 7 missing
3 │ 4 6 missing
7. 実践:全世界のコロナの感染データ (課題4:基礎)
全世界のコロナの感染データ
小規模な big data として、「学術に使って良い」Covid-19 の感染データを扱ってみます。
ホームページはこちら: https://ourworldindata.org/coronavirus-data
• データファイル: owid-covid-data.csv
• データが毎日更新される。
• ファイルサイズ >40 MB (2022年1月16日の時点)
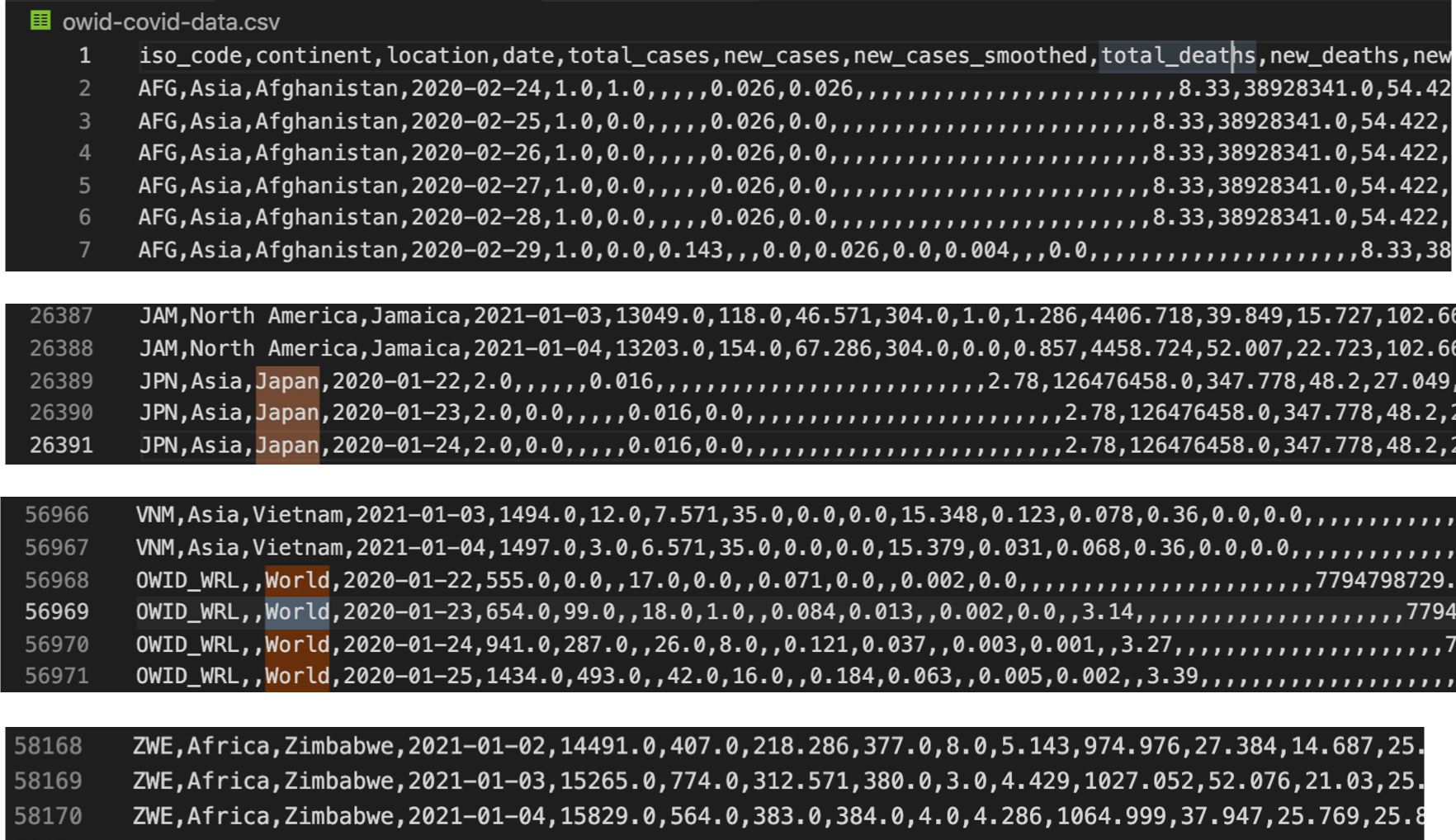
• Afghanistan から Zimbabwe まで、毎日の感染データが収録される。
• 「World」という「世界全体」のデータも入っている。
• よく使う列の項目:
► location 場所「国または自治区」
► date 年月日
► total_cases 日総感染件数
► new_cases 日新感染件数
► total_deaths 日総死者件数
► new_deaths 日新死者件数
► new_tests 日新検査件数
*実習課題4:全世界のコロナの感染データを分析してみる
• 2020年から
► owid-covid-data_2022_01_16.csv (43.6 MB)
上記のファイル、またはホームページから最新のデータを作業フォルダーに保存する。
ファイルを読み込む:
生データ = CSV.read("owid-covid-data_2022_01_16.csv" , DataFrame)
show(生データ)
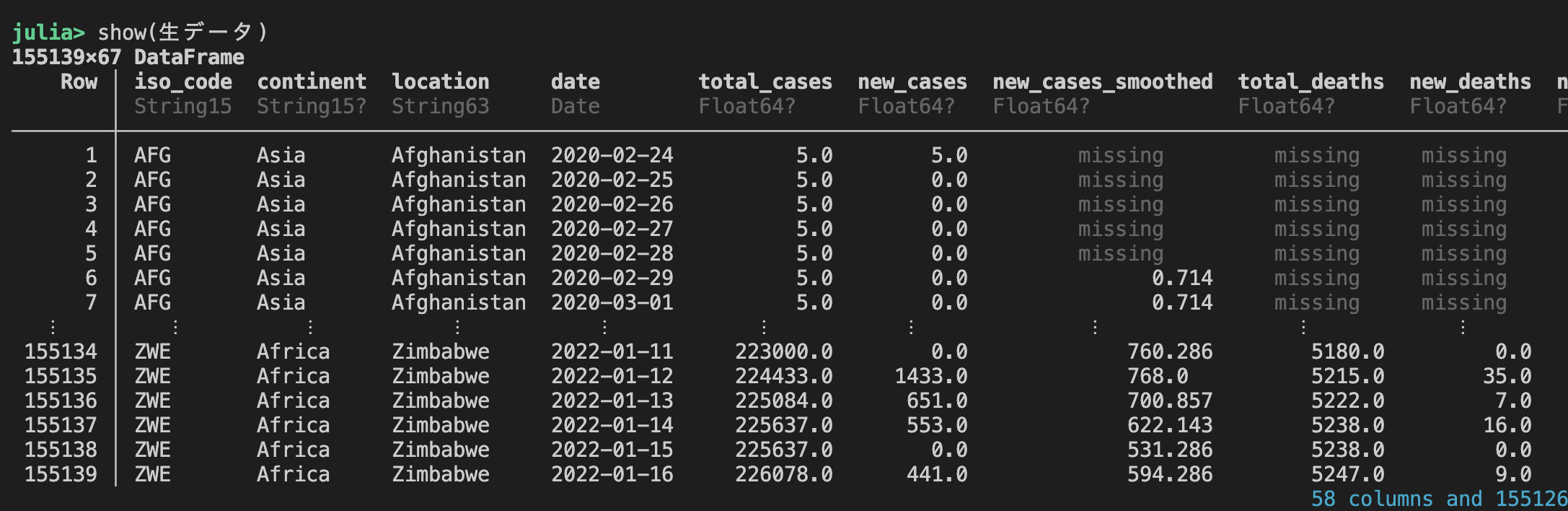
「世界」のデータを読み込まない:
#location = World 「世界」という「全体の合計データ」も入っている。
#そのほか、国別ではないデータも排除する。
A = 生データ[ 生データ.location .!= "World" ,:] #「全世界」を排除する
A = A[A.location .!= "High income" , :] #「高所得国」を排除する
A = A[A.location .!= "Upper middle income" , :] #「中高収入」
A = A[A.location .!= "middle income" , :] #「中所得国」
A = A[A.location .!= "Lower middle income" , :] #「低中所得国」
A = A[A.location .!= "Lower income" , :] #低所得国」
A = A[A.location .!= "Europe" , :]
A = A[A.location .!= "North America" , :]
A = A[A.location .!= "Asia" , :]
A = A[A.location .!= "European Union" , :]
A = A[A.location .!= "South America" , :]
A = A[A.location .!= "Africa" , :]
日本のデータを抽出する:
#日本のデータだけ抽出する
日本 = A[A.location .== "Japan" , :]
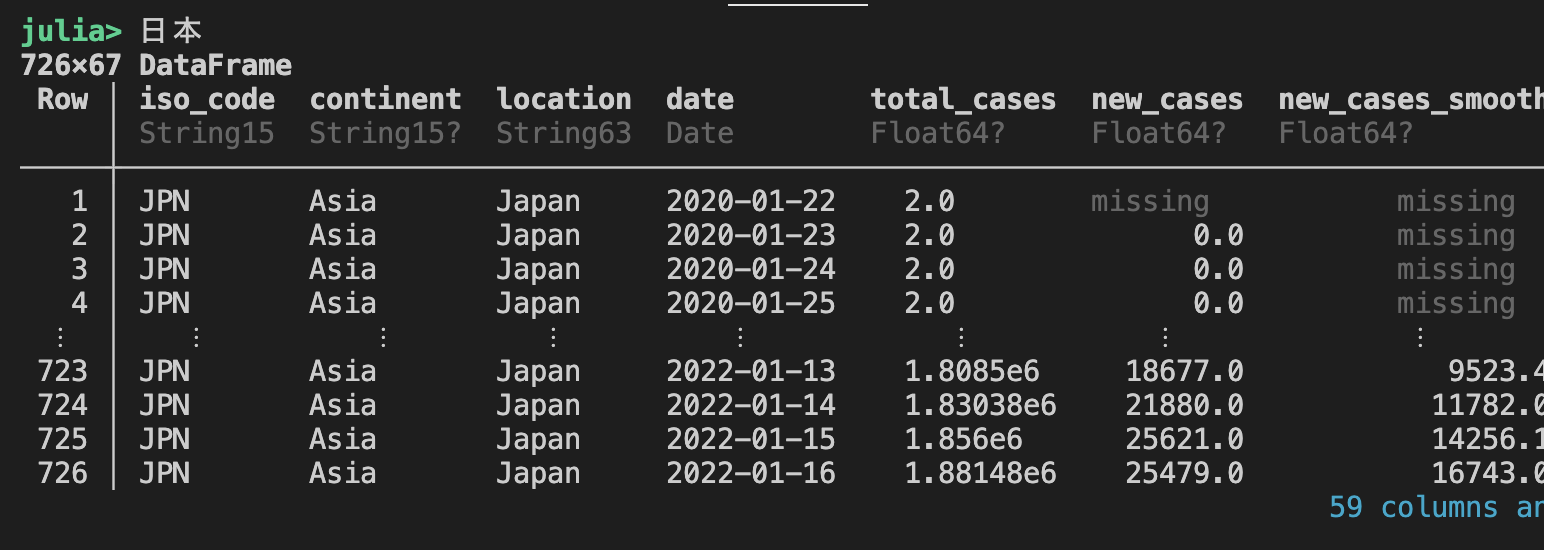
#日本のデータをプロットする
plot(
plot(日本.date, 日本.new_cases,
title = "new cases" ),
plot(日本.date, 日本.total_cases/10000 , title = "total cases" , ylabel = "x 10^4" ),
layout = (2,1 ), legend=false
)
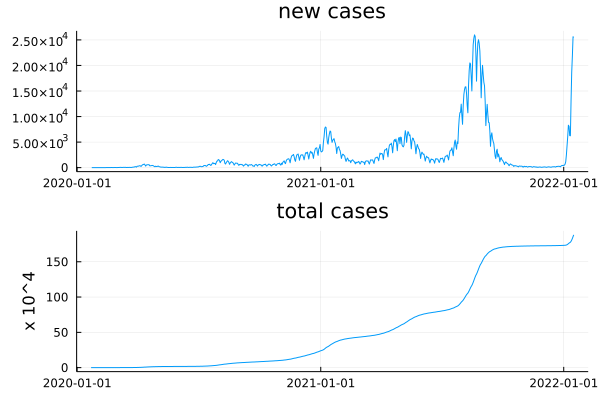
アメリカ、マレシアのデータを抽出する:
US = A[A.location .== "United States" , :]
MY = A[A.location .== "Malaysia" , :]
plot(
plot(日本.date, 日本.new_cases/1000 , label = "JP" ),
plot(US.date, US.new_cases/1000 , label = "US" ),
plot(MY.date, MY.new_cases/1000 , label = "MY" ),
layout = (3,1 ), legend = :topleft,
ylabel = "x 1000"
)
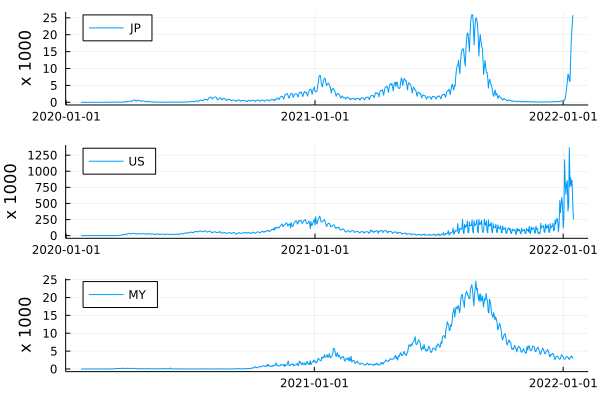
8. 実践:全世界のコロナの感染データ (課題5:日付けの範囲)
*実習課題5
日付けの関数 Date() を用いる実習:
ある日のデータだけ抽出する
現時点 = A[A.date .== Date(2022,1 ,6 ), :]
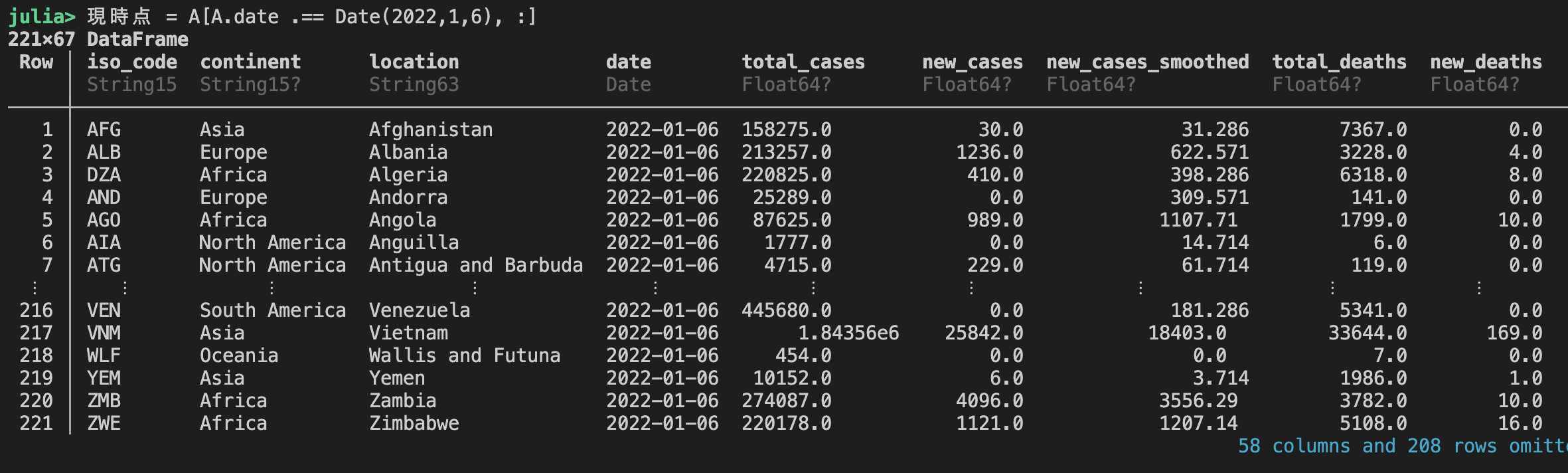
現時点の新規感染件数(多い国から)を表示する
#new_cases でソーティングを行う。逆順:多いから並ぶ
Top = sort(現時点, :new_cases, rev = true)
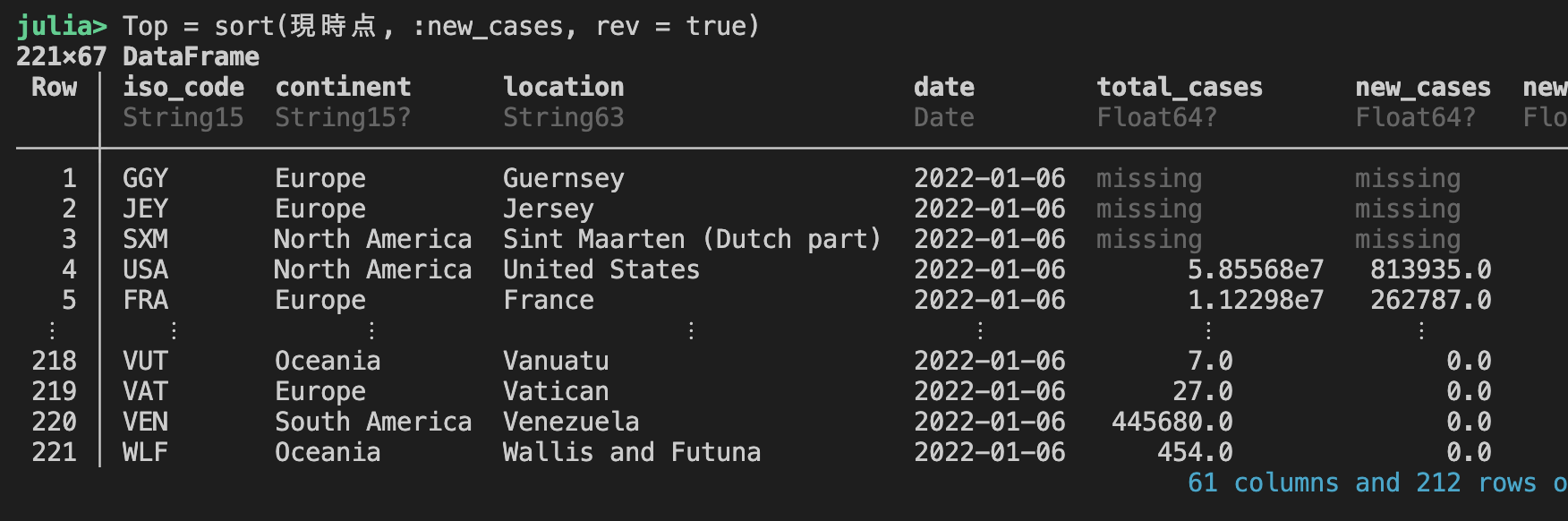
missing のデータを排除して、Top 15を抽出する
Top = dropmissing(Top, :new_cases)
Top = Top[1:15 , :]
bar(Top.location, Top.new_cases/10000 ,
legend = false,
ylabel = "x 10^4" ,
xrotation = 45 ,
)
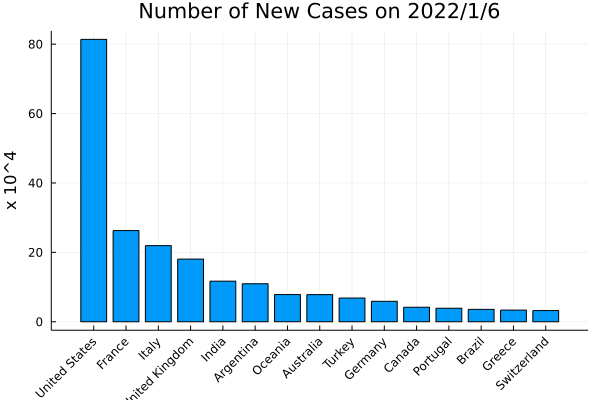
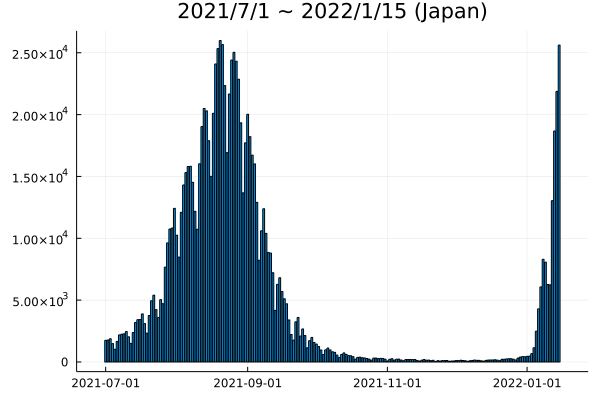
日付け範囲を絞って、日本のデータをもう一度プロットする:
日本 = A[A.location .== "Japan" , :]
B = 日本[(日本.date .>= Date(2021,7 ,1 )) .& (日本.date .<= Date(2022 , 1 , 15 )), : ]
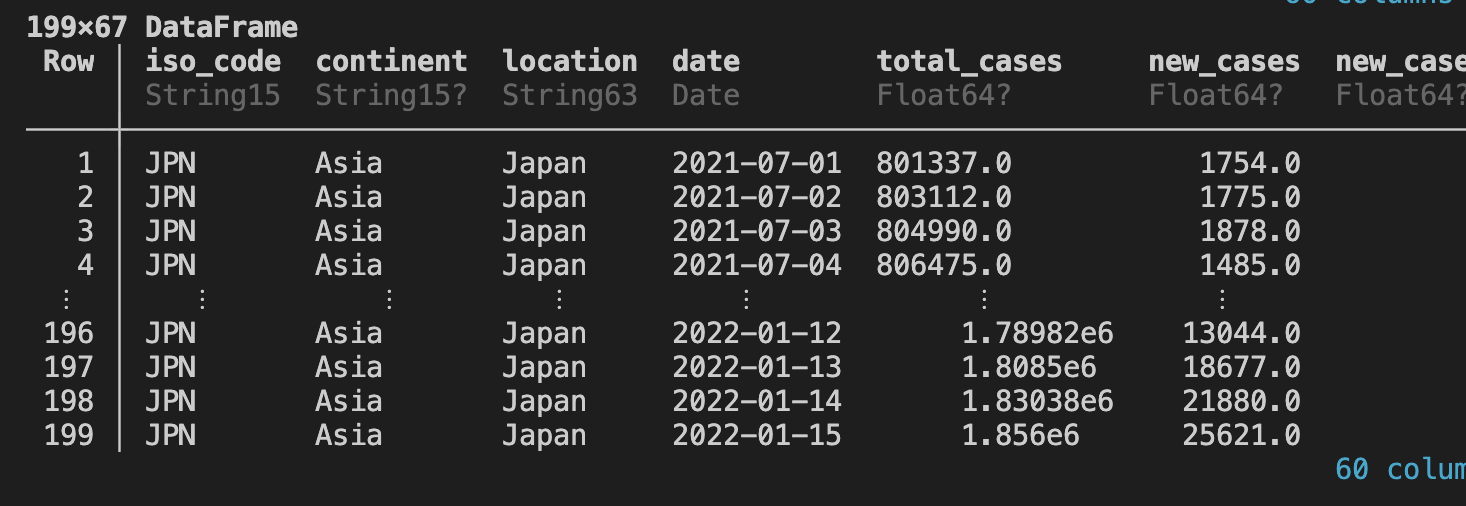
bar(B.date, B.new_cases,
legend = false,
title = "2021/7/1 ~ 2022/1/15 (Japan)" )