データサイエンス CDS009    (チェン leechuin@yamanashi.ac.jp)　更新日: 2022-10-01

---

データの型＆配列演算

1. Julia ターミナル(REPL)の操作 Tips

 • 矢印 キー ↑ と ↓ で一度実行した指令を呼び出せる。

 • 矢印 キー ← と → で呼び出した過去の指令を修正して、新しい指令にすることができる。

---

2. Data Type データの型

Primitive type プリミティブ型, 基本型 組み込み型

Int: Integer 整数

        ► 例：-2, -1, 0, 1, 2

UInt : Unsigned Integer 符号なし整数

 • 通常、１６進数で表すことが多い。

        ► 例：1, 2 ...

        ► 例：0x1f, 0x2e

Float : Floating point 浮動小数点数

        ► 例：1.2, 2.0

Bool : Boolean ブーリアン型

        ► 例：true（真）, false（偽）

Char: Character 文字（１つだけ）

        ► Single quote シングルクォーテーション、単一引用符 で表す。

        ► 例：'a'

---

Non-primitive type 他の型

String: String 文字列

        ► Double quote ダブルクォート 二重引用符で表す。

        ► 例："abe"

Complex : Complex number 複素数

        ► 例：3 + 4im

        ► im は i = √−1 のこと。

Array: Array 配列

        ► [...] で表す。

        ► 例（整数だけの列）：[1, 2, 3]

        ► 例（数値の列）：[1.2, 2.0, 3]

        ► 例（数値と文字などの列）：[1.2, ”abe”, 3]

        ► 例（数値列の列）：[ [1, 2, 3], [1, 1, 1] , [2, 2, 2] ]

Dict : Dictionary　辞書

        ► 例："a"=> 1, "b"=> 20, "c" => "100"

        ► 例："apple"=> "リンゴ", "big"=> "大きい", "cat" => "ネコ"

---

練習：変数の定義、再定義、変数の型の確認

 • 同じ名前の変数を再定義することができる。

 • 再定義したら、変数の型も変わる。

 • 関数 typeof で変数の型の確認ができる。

julia> x = 1 #整数
1

julia> typeof(x)
Int64

julia> x = 1.1 #浮動小数点
1.1

julia> typeof(x)
Float64

julia> x = 3 + 4im #複素数
3 + 4im

julia> abs(x) #xの絶対値 absoluteのこと
5.0

julia> typeof(x)
Complex{Int64}

julia> 3 > 4
false

julia> x = 4 > 3 #Boolean
true

julia> typeof(x)
Bool

julia> x = 'a' #文字
'a': ASCII/Unicode U+0061 (category Ll: Letter, lowercase)

julia> typeof(x)
Char

julia> x = "abe" #文字列
"abe"

julia> typeof(x)
String

julia> x = [1, 2, 3] #配列
3-element Array{Int64,1}:
 1
 2
 3

julia> typeof(x)
Array{Int64,1}

julia> x = Dict("apple"=> "リンゴ", "big"=> "大きい", "cat" => "ネコ") #辞書
Dict{String, String} with 3 entries:
  "cat"   => "ネコ"
  "big"   => "大きい"
  "apple" => "リンゴ"

julia> x["cat"]
"ネコ"

julia> typeof(x)
Dict{String, String}

---

3. データの更新

数学言語では下記の数式の「文法」は正しくない。

\[ x = x + 1 \]

下記の方が意味が通じる。

\[x_{new} = x_{old} + 1\]

数学言語とは違って、プログラミング言語では、変数の更新は下記のような式を使います。

        ► x = x + 1

＊実習：変数の更新

julia> x = 1
1

julia> x = x + 1
2

julia> x = x * 2
4

julia> x = x ^ 2
16

Updating operators という変数の更新用の演算子があります。

julia> x = 1
1

julia> x += 1 # x = x + 1 と同じ 
2

julia> x *= 3
6

julia> x ^= 2
36

---

4. 配列の長さ、サイズ、要素を取り出す

＊実習：要素の数とサイズ

関数 length()で配列の長さ（要素の数）の確認ができる。

関数 sizeof()で配列の Byte数 の確認ができる。

julia> x = [5, 6, 7, 8, 9];

julia> length(x)
5

julia> sizeof(x) #１整数は８bytesです。
40

＊実習：要素の取り出す

julia> x = [5, 6, 7, 8, 9];

julia> x[1]
5

julia> x[2]
6

julia> x[end]
9

＊実習：Range で一部の要素を取り出す

 •  Start:End

        ►  Start の位置から、End 位置までの要素を取り出す

        ►  Step の増分は＋１

 •  Start:Step:End

        ►  Start の位置から、Step 間隔で、Endの位置まで要素を取り出す

julia> x = [5, 6, 7, 8, 9];

julia>  x[1:3]
3-element Array{Int64,1}:
 5
 6
 7

julia> x[2:4]
3-element Array{Int64,1}:
 6
 7
 8

julia> x[1:2:5] #間隔は２です
3-element Array{Int64,1}:
 5
 7
 9

---

5. 配列の最大、最小値、合計値 maximum, minimum, sum

練習:該当の値を取り出す・算出

julia> x = [3, 2, 1, 6, 5, 4]
6-element Array{Int64,1}:
 3
 2
 1
 6
 5
 4

julia> maximum(x) #最大値
6

julia> minimum(x) #最小値
1

julia> sum(x) #合計値
21

練習:最大・最小値のの位置

関数 argmax : argument maximum の省略。 最大値を出力する入力の値

関数 argmin : argument manimum の省略。 最大値を出力する入力の値

julia> x = [3, 2, 1, 6, 5, 4]
6-element Array{Int64,1}:
 3
 2
 1
 6
 5
 4

julia> argmax(x)
4

julia> argmin(x)
3

---

6. 配列の演算　dot-operation

Juliaの１次元配列はベクトル (Vector)である。

練習：加減算

同じサイズのベクトルならば、下記の加減算ができる。

\[\begin{pmatrix}~1~\\2\\3\end{pmatrix}+\begin{pmatrix}~4~\\5\\6\end{pmatrix}=\begin{pmatrix}~5~\\7\\9\end{pmatrix}\]

\[\begin{pmatrix}~4~\\5\\6\end{pmatrix}-\begin{pmatrix}~1~\\2\\3\end{pmatrix}=\begin{pmatrix}~3~\\3\\3\end{pmatrix}\]

julia> x = [1, 2, 3]; #結果を表示しないように

julia> y = [4, 5, 6];

julia>  x + y
3-element Array{Int64,1}:
 5
 7
 9

julia> y - x
3-element Array{Int64,1}:
 3
 3
 3

但し、ベクトルとスカラーとの加減算ができない。

\[\begin{pmatrix}~1~\\2\\3\end{pmatrix}+1=❓❗\]

julia>  x + 1
ERROR: MethodError: no method matching...

dot-plus .+ または dot-minus .-を使えば、各様要素の演算ができる

julia> x .+ 1
3-element Array{Int64,1}:
 2
 3
 4

練習：乗除算

ベクトルはスカラーの乗除算はでき。

\[2\begin{pmatrix}~1~\\2\\3\end{pmatrix} = \begin{pmatrix}~2~\\4\\6\end{pmatrix}\]

julia> x = [1, 2, 3];

julia> 2 * x
3-element Array{Int64,1}:
 2
 4
 6

但し、ベクトルとベクトルの通常的な掛け算と割り算ができない。

\[\begin{pmatrix}~1~\\2\\3\end{pmatrix}\begin{pmatrix}~4~\\5\\6\end{pmatrix}=❓❗\]

julia> x = [1, 2, 3];

julia> y = [4, 5, 6];

julia> x * y
ERROR: MethodError: no method matching...

＊実習 Dot Operation

次の例を参考にして、配列の　element wise operation (要素ことの演算)を行う。

julia> x .* y
3-element Array{Int64,1}:
  4
 10
 18

julia> y ./ x
3-element Array{Float64,1}:
 4.0
 2.5
 2.0

julia> x .^2
3-element Array{Int64,1}:
 1
 4
 9

---

7. 配列の演算 Broadcasting

 • Broadcast は放送の意味です。

 • 例：f.(X)

 • f はある関数。X は配列。

 • 直訳では 「その関数を配列中の各要素に放送する。」

 • 意味は「配列中の各要素を　その関数で演算・実行する。」

 • 注意点： 先ほどの dot-operation と違って、これは function-dot です。

＊練習：既存の内部関数

julia> x = [0, 1, 2, 3]
4-element Array{Int64,1}:
 0
 1
 2
 3

julia> sin(x) #xは配列なので、これは使えません
ERROR: MethodError: no method matching sin(::Array{Int64,1})

julia> sin.(x)
4-element Array{Float64,1}:
 0.0
 0.8414709848078965
 0.9092974268256817
 0.1411200080598672

＊実習：自分なりの関数

下記の例にある exp(x) は指数関数のことです：\[\exp(x)=e^{x}\]

julia> f(x) = exp(x) + sin(x) + cos(x) #自分の関数を使ってください。
f (generic function with 1 method)

julia> y = [0, 0.1, 0.5, 1]
4-element Array{Float64,1}:
 0.0
 0.1
 0.5
 1.0

julia> f.(y)
4-element Array{Float64,1}:
 2.0
 2.200008500000502
 3.005729371194704
 4.100055119135082

---

8. １次元配列の自動作成：順列、逆列

練習：間隔が１の配列

関数 Array(start : end)　または Vector(start : end) があります。

どれを使ってもOKです。

julia> x = Array(1:4)
4-element Array{Int64,1}:
 1
 2
 3
 4

julia> y = Vector(1:4)
4-element Array{Int64,1}:
 1
 2
 3
 4

julia> x == y #xとyは同じものですか？
true

練習：間隔が１ではない配列

関数 Array(start : step : end)　または Vector(始 : 間隔 : 終) を使います。

julia> x = Array(1:0.5:4)
7-element Array{Float64,1}:
 1.0
 1.5
 2.0
 2.5
 3.0
 3.5
 4.0

julia> y = Vector(1:0.2:4)
16-element Array{Float64,1}:
 1.0
 1.2
 1.4
 1.6
 1.8
 ⋮
 3.2
 3.4
 3.6
 3.8
 4.0

julia> x == y #xとyは同じものですか？
false

逆順

次ののはダメの例です。

４から０までの配列を作りなさいという指令ですが、増分が指定されなかったので、無効となります。

Errorが出なかったが、その出力は　空の配列です。

julia> Array(4:0)
Int64[]

有効の例はこちら：

julia> Array(4:-1:0)
5-element Array{Int64,1}:
 4
 3
 2
 1
 0

＊実習：問題

下記の配列を作成してください。

julia> x = ❓
81-element Array{Float64,1}:
 -4.0
 -3.9
 -3.8
 -3.7
 -3.6
  ⋮
  3.6
  3.7
  3.8
  3.9
  4.0

---

9. 配列の自動作成：乱数列

ここで、関数 rand() と関数 randn() を紹介します。

練習：rand 連続一様分布（一様乱数）

 • 区間内で全ての実数が同じ確率

 • 使い方：

        ► 何にもを指定しない : rand()　→ 0 から 1 までの小数

        ► Range を指定する : rand(0:5)　→ 0 から 5 までの整数

        ► Range を細く指定する : rand(0:0.2:5) 　→ 0 から 5 まで 0.2 刻みの数値

julia> x = rand()
0.44460327301965363

julia> x = rand()
0.7403324908844962

julia> x = rand(0:5)
3

julia> x = rand(0:5)
2

julia> x = rand(0:0.2:5)
2.8

練習：rand(N) 連続一様分布（一様乱数）の列

 • N は要素の数

 • 使い方：

        ► Range を指定しない : rand(5)　→ 0 から 1 までの小数, 5個を作ります。

        ► Range を指定する : rand(0:5, 5)　→ 0 から 5 までの整数

        ► Range を細く指定する : rand(0:0.2:5, 5) 　→ 0 から 5 まで 0.2 刻みの数値

julia> rand(5)
5-element Array{Float64,1}:
 0.7057209159690532
 0.6956097711557745
 0.4808145616806476
 0.5792035947895804
 0.9646441158364953

julia> rand(0:5, 5)
5-element Array{Int64,1}:
 0
 0
 1
 4
 3

julia> rand(0:0.2:5, 5)
5-element Array{Float64,1}:
 1.6
 0.0
 0.6
 4.8
 4.6

Range の他に、配列の中の要素

julia> rand(["グー　✊", "チョキ✌", "パー　✋"], 5)
5-element Array{String,1}:
"パー　✋"
"チョキ✌"
"チョキ✌"
"グー　✊"
"パー　✋"

練習：randn 標準正規乱数とその列

 • N は要素の数

 • 標準正規分布（平均値＝０、標準偏差＝１）の乱数と乱数列を作成する。

 • 使い方：

        ► N を指定しない : randn()　→ 平均値 0, 標準分布 1 の乱数, 1個。

        ► N を指定する : randn(5)　→ 標準正規分布乱数の列。要素の数＝５。

julia> x = randn()
0.9191868812042517

julia> x = randn(100)
100-element Array{Float64,1}:
  0.1911516472510612
  0.0016521419110062643
 -0.5662498378908175
  1.2185659120575463
  1.2006481191590448
 -0.3709526966710927
  ⋮
  0.34430045006801746
 -0.30211629318059696
  1.6252578782188407
 -0.4811986209483117
 -1.355658000401184

julia> sum(x)/100 #平均値を確認してみる
-0.09335189446868274

---

10. 簡単のグラフを描いてみる

 • 外部の Plots という Packageを使います。

 • Julia はまた開発中で、time-to-first-plot という未解決の問題点があります。

 • 初回の plot には時間がかかる

 • ２回目以降は　通常の速度となります。

 • Plots の中に ２つの backend (裏のプログラム) が入っている。

 • gr()

        ► デフォルト、軽い、簡易、表示が早い、日本語未対応。

 • plotly()

        ► 表示がちょっと遅い、browserを使う、日本語対応、ある企業の製品（無償）

練習

julia> using Plots #この指令は一回だけ実行する。

julia> x = Array(-4:1:4);

julia> y = x .^2;

julia> plot(x, y)

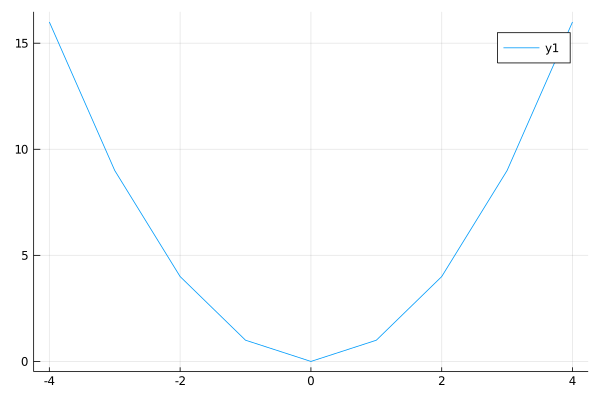
＊実習：滑やなのグラフ

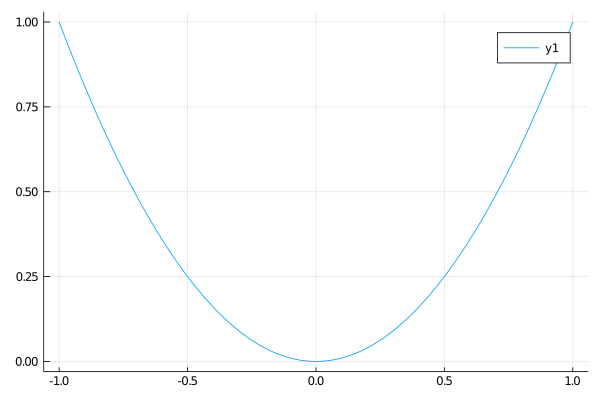
下記なめやかなグラフを描いてください。

julia> x =　❓ 

julia> y = ❓ 

julia> plot(x, y)

指令だけワードにまとめてください。

グラフの貼り付けは不要。

11. Append Graph グラフを重ねる

 • 関数 plot() は新規のグラフを作成する。

 • 関数 plot!() は既存のグラフに新しいグラフを追加する。

julia> theta = Array(0 : pi/100 : 2*pi);

julia> plot(theta, sin.(theta))

julia> plot!(theta, cos.(theta))

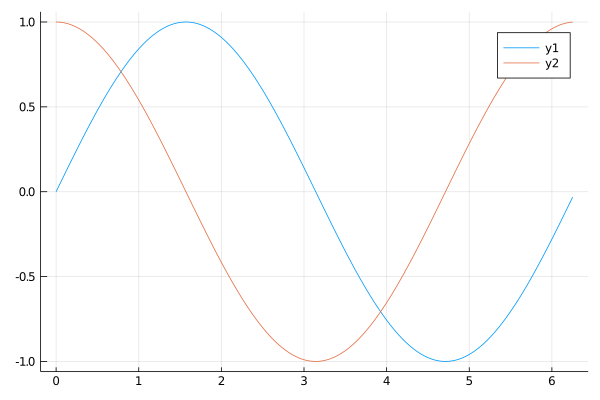
＊実習：標準正規分布乱数を使って、下記のグラフを作成する

 • plotly() を使ってみる。

julia> plotly()

julia> theta = Array(0 : pi/100 : 2*pi);

julia> N = length(theta)

julia> Noise = 0.5 * ❓

julia> Y  = ❓

julia> plot(theta, Y + Noise)

julia> plot!( ❓ )

julia> plot!(xlabel = "位相角", ylabel = "信号強度")

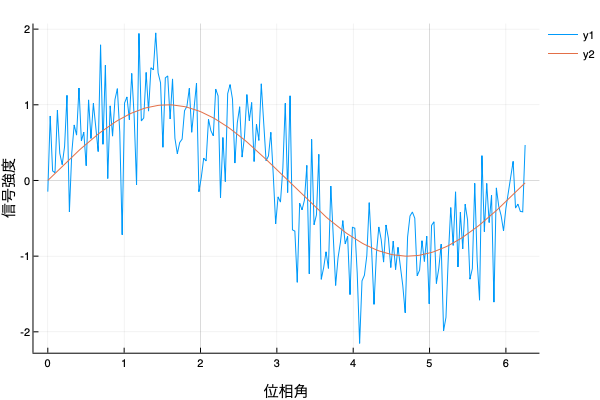
作成したグラフをダウンロードして、ワードに挿入してください。

---

追加情報：写真の挿入

作成したグラフの「ダウンロード」ができる。

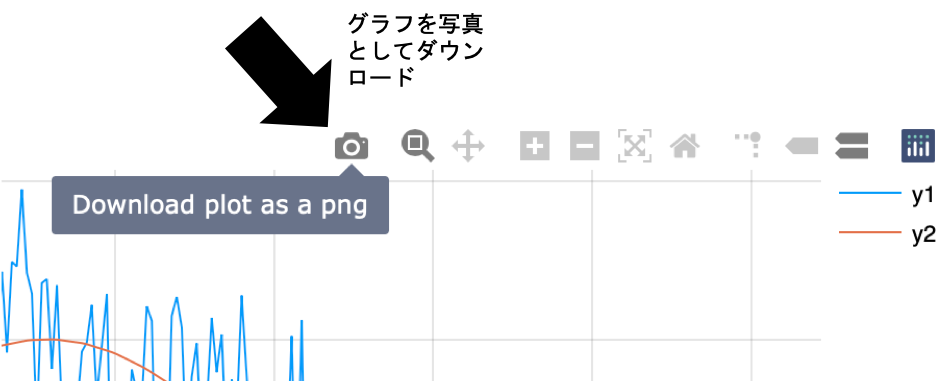
ワードに「写真の挿入」ができる。

---

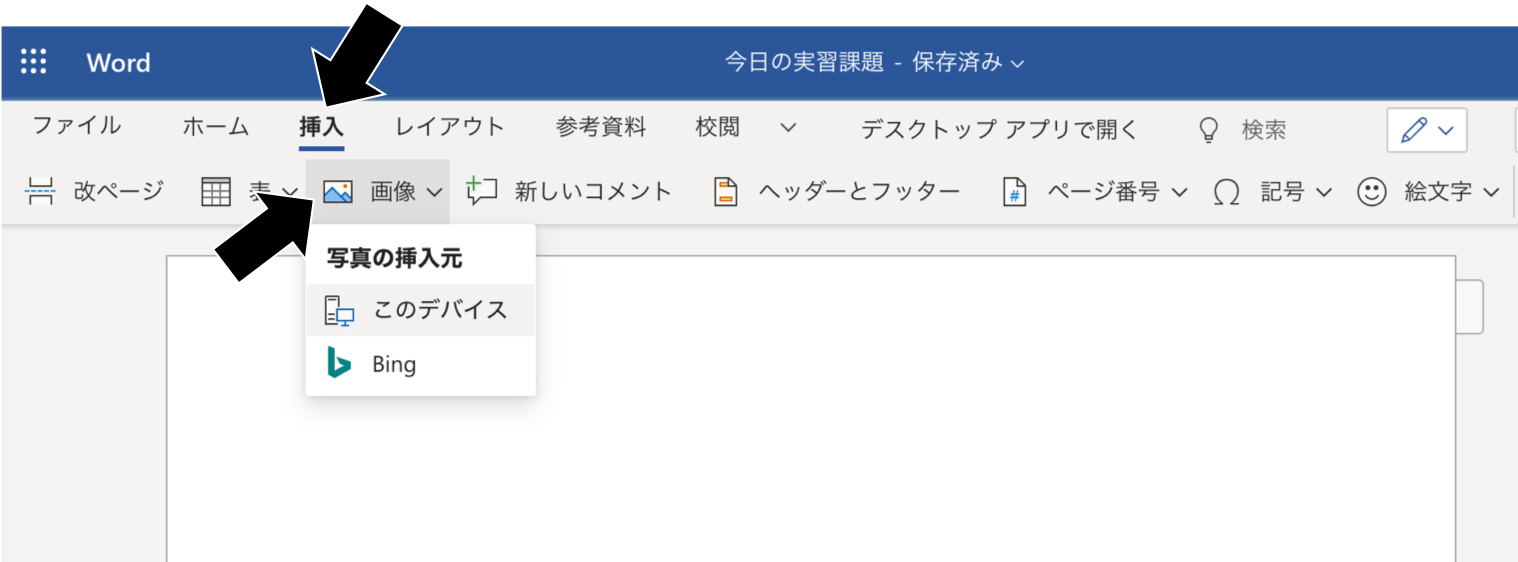
追加情報：上記 plotly の方法が使えない場合。

Plotly が使えない可能性がある。

その場合、 gr() に切り替えて、 savefig で plot した図形を保存する。

gr()は日本語の入力が出来ない。

julia> gr()

julia> theta = Array(0 : pi/100 : 2*pi);

julia> N = length(theta)

julia> Noise = 0.5 * ❓

julia> Y  = ❓

julia> plot(theta, Y + Noise)

julia> plot!( ❓ )

julia> plot!(xlabel = "Angle", ylabel = "Intensity")

julia> savefig("myfig.png") #図形を保存する。

保管場所は次の指令で調べられす。

julia> pwd()