データサイエンス CDS009 (チェン leechuin@yamanashi.ac.jp)　更新日: 2022-10-01

応用線形代数 I

線形代数の例：

\[ a_1 x_1 + a_2 x_2 \cdots + a_n x_n = y \]

線形代数ではないの例：

\[ \frac{a_1 x_1 + a_2 x_2 \cdots + a_n x_n}{b_1 x_1 + b_2 x_2 \cdots } = y \]

1. ＊実習課題のグラフの保存方法について

＊実習と書かれた部分はワードにまとめてください。

使用するパケージ

今回の授業は Plots と線形代数用の関数を使うので、下記の指令を一度実行してください。

julia> using LinearAlgebra #これは内蔵されたパケージです。

julia> using Plots　#前回使った plot の追加パケージです。

Julia ターミナル(REPL)の操作 Tips

• 矢印キー ↑ と ↓ で一度実行した指令を呼び出せる。

• 矢印キー ← と → で呼び出した過去の指令を修正して、新しい指令にすることができる。

グラフ

グラフは「挿入」でワードに載せてください。

• Plots のパケージには、２つの裏プログラム(backend): gr と　plotly がある。

• plotly() で plotly を指定する。

► plotly は日本語の表示ができる。

► 初期の指定が必要です。

• gr() で gr を指定する。

► デフォルトの backend となる。初期の指定は必要ない。

► plotly より、処理が早い。

► gr で作成したグラフは関数 savefigで保存できる。

julia> savefig("ファイル名.png")

• ファイルの保存先は　Julia の「作業フォルダー」となります。

• 「作業フォルダー」は関数 pwd で調べられる。

julia> pwd()
"/Users/leechuin/Documents/データサイエンス_2020/Topic4_MatrixOperation"

pwd() は Print Working Directory 「作業フォルダーを印刷・表示」するという指令です。

2. Vector and Matrix ベクトルと行列

ベクトル

例１：

\[ \mathbf{a} = \hat{\mathbf{x}} + 2\hat{\mathbf{y}} + 3\hat{\mathbf{z}} = \begin{pmatrix} ~1~ \\2\\3 \end{pmatrix}\]

Julia は一次元の配列を「ベクトル」として扱っています。

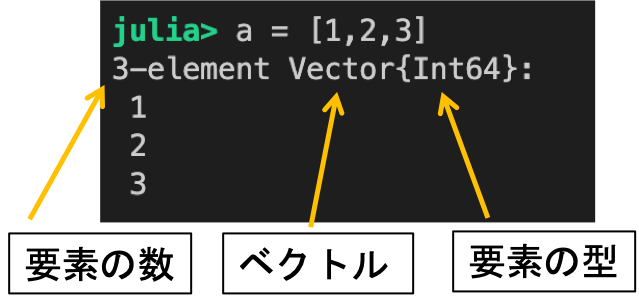
行列

例１\(1\times3\),\(2\times2\),\(2\times3\)の行列：

\[\begin{pmatrix}~1 & 2 & 3~\end{pmatrix} ,~~\begin{pmatrix}~1 & 2 \\ 3 & 4~\end{pmatrix}, ~~\begin{pmatrix}~1 & 2 & 3 \\ 3 & 4 & 5~\end{pmatrix}\]

例２\( m\times n \) 行列：

\[ \begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n}\\a_{21} & a_{22} & \cdots & a_{2n}\\\vdots & \vdots & \ddots & \vdots\\a_{m1} & a_{m2} & \cdots & a_{mn}\end{pmatrix} \]

Julia は多次元の配列を行列として扱っています。

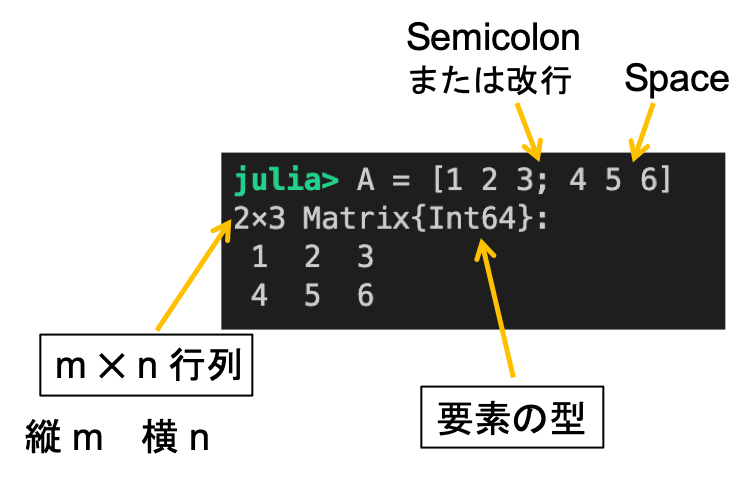
練習：ベクトルと行列の定義

julia> a = [1, 2, 3] #これはベクトルです。
3-element Array{Int64,1}:
1
2
3

julia> B = [1 2 3] #これはベクトルではなく,行列です。
1×3 Array{Int64,2}:
1  2  3

julia> A = [1 2
3 4]
2×2 Array{Int64,2}:
1  2
3  4

julia> A = [1.1 1.2 1.3; 2.1 2.2 2.3; 3.1 3.2 3.3]
3×3 Array{Float64,2}:
1.1  1.2  1.3
2.1  2.2  2.3
3.1  3.2  3.3

3. 行列の自動作成

Zeros & Ones

関数 zeros

• zeros(n)：零ベクトル. n ：要素の数

• zeros(m, n)：零行列. m：行数、n：列数

julia> zeros(4)
4-element Array{Float64,1}:
 0.0
 0.0
 0.0
 0.0

julia> zeros(4,4)
4×4 Array{Float64,2}:
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0
 0.0  0.0  0.0  0.0

関数 ones

• ones(n)：成分は全て１のベクトルを作成。 n：要素の数

• ones(m, n)：成分は全て１の行列を作成。 m：行数、n：列数

julia> ones(3)
3-element Array{Float64,1}:
 1.0
 1.0
 1.0

julia> ones(2,3)
2×3 Array{Float64,2}:
 1.0  1.0  1.0
 1.0  1.0  1.0

4. 多次元行列の要素・部分を取り出す方法

２次元行列

要素を取り出す

julia> A = [1 2 3; 4 5 6; 7 8 9]
3×3 Array{Int64,2}:
 1  2  3
 4  5  6
 7  8  9

julia> A[1,1] #縦１、横１の要素
1

julia> A[2,1] #縦２、横１
4

julia> A[2,2]
5

部分を取り出す

julia> A = [1 2 3; 4 5 6; 7 8 9]
3×3 Array{Int64,2}:
 1  2  3
 4  5  6
 7  8  9

julia> A[1,:] #縦１, 横は全て
3-element Array{Int64,1}:
 1
 2
 3

julia> A[:,2] #縦 all, 横２
3-element Array{Int64,1}:
 2
 5
 8

julia> A[3, 2:3] #縦３, 横は ２から３
2-element Array{Int64,1}:
 8
 9

３次元行列

julia> A=zeros(2,2,2) #まずは行列の形を定義する。
2×2×2 Array{Float64,3}:
[:, :, 1] =
0.0  0.0
0.0  0.0

[:, :, 2] =
0.0  0.0
0.0  0.0

julia> A[:, :, 1] = [1 2 ; 3 4] #2次元の部分を手動で定義する。
2×2 Array{Int64,2}:
1  2
3  4

julia> A[:, :, 2] = [5 6 ; 7 8] #もう１つ2次元の部分を定義する。
2×2 Array{Int64,2}:
5  6
7  8

julia> A
2×2×2 Array{Float64,3}:
[:, :, 1] =
1.0  2.0
3.0  4.0

[:, :, 2] =
5.0  6.0
7.0  8.0

julia> A[2,2,1]
4.0

julia> A[1,2,2]
6.0

5. 行列の積

A と B 行列があって、A の列数と B の行数が等しいであれば AB が定義される。

例えば A が (m × n) 行列で、B が (n × p) 行列で、AB が (m × p) の行列となる。

\[\mathbf{AB} = \begin{pmatrix}\color{darkred} a_{11} & \color{darkred} a_{12} & \cdots & \color{darkred} a_{1n} \\\color{darkgreen} a_{21} & \color{darkgreen}a_{22} & \cdots & \color{darkgreen}a_{2n} \\\color{black} \vdots & \vdots & \ddots & \vdots \\\color{darkblue} a_{m1} & \color{darkblue} a_{m2} & \cdots & \color{darkblue} a_{mn} \\\end{pmatrix}\begin{pmatrix}\color{darkred} b_{11} & \color{darkgreen} b_{12} & \cdots & \color{darkblue}b_{1p} \\\color{darkred} b_{21} & \color{darkgreen} b_{22} & \cdots & \color{darkblue}b_{2p} \\\color{darkred} \vdots & \color{darkgreen} \vdots & \ddots & \color{darkblue}\vdots \\\color{darkred} b_{n1} & \color{darkgreen} b_{n2} & \cdots & \color{darkblue}b_{np} \\\end{pmatrix} = \begin{pmatrix}\color{darkred} c_{11} & c_{12} & \cdots & c_{1p} \\c_{21} & \color{darkgreen}c_{22} & \cdots & c_{2p} \\\vdots & \vdots & \ddots & \vdots \\c_{m1} & c_{m2} & \cdots & \color{darkblue}c_{mp} \\\end{pmatrix}\]

\[ c_{ij} = a_{i1}b_{1j} + a_{i2}b_{2j} + \cdots + a_{in}b_{nj} = \sum_{k=1}^{n}a_{ik}b_{kj}\]

練習：簡単の例

\[\begin{pmatrix}1 & 2 \\3 & 4\end{pmatrix}\begin{pmatrix}~5~\\6\end{pmatrix} = \begin{pmatrix}1\cdot5 + 2\cdot6\\3\cdot5 + 4\cdot6\end{pmatrix}=\begin{pmatrix}17\\39\end{pmatrix}\]

julia> [1 2 ; 3 4] * [5 ; 6]
2-element Array{Int64,1}:
 17
 39

＊実習：Juliaを使って、次の計算を行う

\[ \mathbf{A} = \begin{pmatrix} 1&2&3 \\4&5&6\\7&8&9\end{pmatrix},~~\mathbf{B} = \begin{pmatrix} 2&7&6 \\9&5&1\\4&3&8\end{pmatrix},~~\mathbf{U} = \begin{pmatrix} 1\\3\\5 \end{pmatrix},~~\mathbf{V} = \begin{pmatrix} 2&4&6 \end{pmatrix}\]

a) \( \mathbf{AB} \)

b) \( \mathbf{BA} \)

c) \( \mathbf{AU} \)

d) \( \mathbf{UV} \)

e) \( \mathbf{VU} \)

6. Transposed Matrix 転置行列

定義：

\[\mathbf{A} = \begin{pmatrix}\color{darkred} a_{11} & \color{darkgreen} a_{12} & \cdots & \color{darkblue}a_{1n} \\\color{darkred} a_{21} & \color{darkgreen} a_{22} & \cdots & \color{darkblue}a_{2n} \\\color{darkred} \vdots & \color{darkgreen} \vdots & \ddots & \color{darkblue}\vdots \\\color{darkred} a_{m1} & \color{darkgreen} a_{m2} & \cdots & \color{darkblue}a_{mn} \\\end{pmatrix},~~~~\mathbf{A}^T = \begin{pmatrix}\color{darkred} a_{11} & \color{darkred} a_{21} & \cdots & \color{darkred} a_{m1} \\\color{darkgreen} a_{12} & \color{darkgreen}a_{22} & \cdots & \color{darkgreen}a_{m2} \\\color{black} \vdots & \vdots & \ddots & \vdots \\\color{darkblue} a_{1n} & \color{darkblue} a_{2n} & \cdots & \color{darkblue} a_{mn} \\\end{pmatrix}\]

• (m × n) の行列を転置 (transpose)したら、 (n × m) の行列になります。

練習：transpose 関数

julia> A = [1 2 3; 4 5 6]
2×3 Array{Int64,2}:
1  2  3
4  5  6

julia> AT = transpose(A)
3×2 LinearAlgebra.Transpose{Int64,Array{Int64,2}}:
 1  4
 2  5
 3  6

練習：対称行列

定義：\(B^T = B\). 例：

\[ \begin{pmatrix}1 & \color{red} 7 & \color{red}3 \\\color{green}7 & 4 & \color{red}5\\\color{green}3 & \color{green}5 & 6\end{pmatrix}\]

対称行列は\(B=A^TA\) で作成できる。

julia> A = rand(0:1, (5,5)) #任意の正方行列を作成
5×5 Array{Int64,2}:
 0  1  0  1  0
 1  1  1  0  0
 0  0  1  1  0
 1  1  0  0  1
 0  1  1  0  0

julia> B = transpose(A)*A　#対称行列を作成
5×5 Array{Int64,2}:
 2  2  1  0  1
 2  4  2  1  1
 1  2  3  1  0
 0  1  1  2  0
 1  1  0  0  1

julia> transpose(B) == B #確認
true

7. ベクトルの内積 (dot product)

内積 (dot product)の定義 (３次元)：

\[\mathbf{a} \cdot \mathbf{b} =\begin{pmatrix}~a_x~\\a_y\\a_z\end{pmatrix}\cdot\begin{pmatrix}~b_x~\\b_y\\b_z\end{pmatrix}= a_x~b_x + a_y~b_y + a_z~b_z\]

内積 (dot product)の定義 (多次元)：

\[\mathbf{a} \cdot \mathbf{b} =\begin{pmatrix}~a_1~\\a_2\\\vdots\\a_m\end{pmatrix}\cdot\begin{pmatrix}~b_1~\\b_2\\\vdots\\b_m\end{pmatrix}= a_1~b_1 + a_2~b_2 + \cdots + a_m~b_m\]

転置行列で内積の計算ができる：

\[ \mathbf{a} \cdot \mathbf{b} = \mathbf{a}^T \mathbf{b} = \begin{bmatrix} a_1 & a_2 &\cdots &a_n\end{bmatrix}\begin{bmatrix} b_1 \\ b_2 \\\vdots \\b_n\end{bmatrix}\]

練習：内積の計算

方法１）関数 sum と .*で内積を算出。

julia> a = [1, 2, 3];

julia> b = [4, 5, 6];

julia> Y = sum( a .* b )
32

方法２：転置行列で算出

julia> transpose(a) * b
32

方法３：関数 dotで内積を算出。

julia> using LinearAlgebra #すでに実行したら、やらなくて良い。

julia> dot(a, b)
32

＊実習：内積の計算時間を比較

大規模の列を使って、内積の計算時間を比較する。

• @time を指令の前に置いたら、実行時間が表示される。

• 先に、乱数の数を下記の例より少なめ、例えば 10^7 にして、パソコンの問題がなければ、この数を10^8にする。

julia> x = rand(10^8) #乱数１億個の列を作成。
100000000-element Array{Float64,1}:
 0.5474144020792362
 0.6168312211817326
 ⋮
 0.538102094829189
 0.958668265292917

julia> @time sum( x .* x ) #方法（１）
 0.500417 seconds (248.22 k allocations: 775.753 MiB, 0.84% gc time)
3.332812374812943e7

julia> @time sum( x .* x ) #2回実行したら、時間が一定の範囲内に落ち着く。
 0.404328 seconds (5 allocations: 762.940 MiB, 11.87% gc time)
3.332812374812943e7

julia> @time transpose(x) * x #方法（２）転置行列の方法
 0.059195 seconds (55.41 k allocations: 3.084 MiB)
3.332812374812948e7

julia> @time transpose(x) * x
 0.043327 seconds (2 allocations: 32 bytes)
3.332812374812948e7

どれが早いですか？

8. 行列式 Determinant

数式の書き方：

\[ \det{\mathbf{A}} = |\mathbf{A}| = \begin{vmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots & \vdots & \ddots & \vdots \\a_{m1} & a_{m2} & \cdots & a_{mn} \\\end{vmatrix}\]

行列式の定義

(2 × 2) 行列の場合：

\[ \begin{vmatrix}a & b \\c & d \\\end{vmatrix} = ad - bc\]

(3 × 3) 行列の場合：

\[ \begin{vmatrix}a & b & c\\d & e & f \\g & h & i \\\end{vmatrix} ~=~ a\begin{vmatrix}e & f \\h & i \\\end{vmatrix}~-~ b\begin{vmatrix}d & f \\g & i \\\end{vmatrix}~+~ c\begin{vmatrix}d & e \\g & h \\\end{vmatrix}\]

(4 × 4) 行列の場合：

\[ \begin{vmatrix}a & b & c & d\\e & f & g & h\\i & j & k & l\\m & n & o & p\\\end{vmatrix} ~=~ a\begin{vmatrix}f & g & h\\j & k & l\\n & o & p\\\end{vmatrix}~-~ b\begin{vmatrix}e & g & h\\i & k & l\\m & o & p\\\end{vmatrix}~+~ c\begin{vmatrix}e & f & h\\i & j & l\\m & n & p\\\end{vmatrix}~-~ d\begin{vmatrix}e & f & g \\i & j & k \\m & n & o \\\end{vmatrix}\]

物理的な意味

例１：ベクトルの絶対値

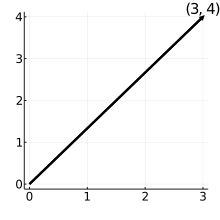
• \( |\vec{A}| = \sqrt{3^2 + 4^2} = 5\) → 長さ

例２：(2 × 2) 行列の行列式

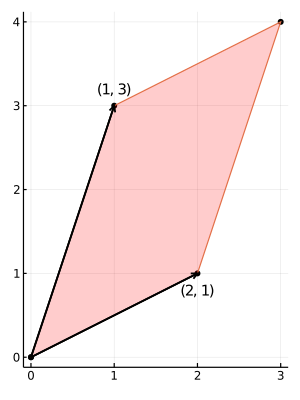
\[ |\mathbf{A}| =\begin{vmatrix}2 & 1 \\1 & 3 \\\end{vmatrix} = 2 \times3 - 1 = 5~~~~→~~面積\]

例３：(3 × 3) 行列の行列式

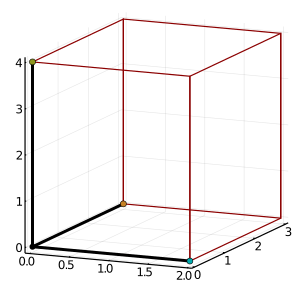
\[ \begin{vmatrix}2 & 0 & 0\\0 & 3 & 0 \\0 & 0 & 4 \\\end{vmatrix} = 2 \times 3 \times 4 = 24~~~~→~~体積\]

性質

\[\det{\mathbf{A}} = \det{\mathbf{A}^T} \]

練習：関数 det

julia> A = [2 0 0; 0 3 0; 0 0 4]
3×3 Array{Int64,2}:
 2  0  0
 0  3  0
 0  0  4

julia> det(A)
24.0

julia> A = rand(0:9, (4,4))
4×4 Array{Int64,2}:
 5  9  9  9
 1  6  8  6
 6  5  2  8
 6  1  1  5

julia> det(A)
-314.0

julia> det(transpose(A))
-314.0

9. 逆行列 Inversed Matrix

\(\mathbf{A}^{-1}\)の定義

\[ \mathbf{A}^{-1} \mathbf{A} = \mathbf{I}\]

\(\mathbf{I}\) は単位行列 Identity Matrix

\[ \mathbf{I} =\begin{pmatrix} 1 & 0 & \cdots & 0\\ 0 & 1 & \cdots & 0\\\vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & 1\\\end{pmatrix}\]

(2 × 2) 行列の場合：

\[ \mathbf{A} = \begin{pmatrix}a & b \\c & d \\\end{pmatrix}\]

\[\mathbf{A}^{-1} = \frac{1}{|\mathbf{A}|}\begin{pmatrix}d & -c \\-b & a \\\end{pmatrix} = \frac{1}{ad - bc}\begin{pmatrix}d & -c \\-b & a \\\end{pmatrix} \]

練習：inv 関数

julia> A = [2 1; 1 3]
2×2 Array{Int64,2}:
 2  1
 1  3

julia> inv(A)
2×2 Array{Float64,2}:
  0.6  -0.2
 -0.2   0.4

＊実習：inv 関数

julia> A = rand(0:9, (4,4))
4×4 Array{Int64,2}:
 5  5  6  4
 8  5  0  6
 4  3  0  4
 8  8  8  7

julia> B = inv(A)
4×4 Array{Float64,2}:
  2.0   0.25    0.25   -1.5
 -8.0   1.0    -4.0     6.0
  2.5  -0.375   1.125  -1.75
  4.0  -1.0     3.0    -3.0

julia> B*A
4×4 Array{Float64,2}:
 1.0  0.0   1.77636e-15  0.0
 0.0  1.0  -7.10543e-15  0.0
 0.0  0.0   1.0          0.0
 0.0  0.0   0.0          1.0

julia> round.(B*A) #四捨五入
4×4 Array{Float64,2}:
 1.0  0.0   0.0  0.0
 0.0  1.0  -0.0  0.0
 0.0  0.0   1.0  0.0
 0.0  0.0   0.0  1.0

10. 線型方程式系 Linear equation system

連立一次方程式とも呼ばれる。

\begin{align}a_{11} x_1 + a_{12} x_2 + \cdots + a_{1n} x_n &= y_1\\a_{21} x_1 + a_{22} x_2 + \cdots + a_{2n} x_n &= y_2\\&\vdots\\a_{n1} x_1 + a_{n2} x_2 + \cdots + a_{nn} x_n &= y_n\end{align}

(n × n)の行列に整理したら

\[\begin{pmatrix}a_{11} & a_{12} & \cdots & a_{1n} \\a_{21} & a_{22} & \cdots & a_{2n} \\\vdots&\vdots & \ddots & \vdots\\a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}=\begin{pmatrix}y_1\\y_2\\\vdots\\y_n\end{pmatrix}\]

簡潔の形：

\[ \mathbf{A}\mathbf{x} = \mathbf{y}\]

一次方程式は逆列の方法で解くことができる。

\[ \mathbf{A}^{-1}\mathbf{A}\mathbf{x} = \mathbf{A}^{-1}\mathbf{y}\]

\[ \mathbf{x} = \mathbf{A}^{-1}\mathbf{y}\]

＊実習：inv を使って連立一次方程式を解く

次の連立一次方程式を解け。

\begin{align}p + 2q + r &= 2\\2p + q + r &= 3\\p + q + 2r &= 3\\\end{align}

julia> A = [1 2 1;2 1 1; 1 1 2] #行列に整理する
3×3 Array{Int64,2}:
 1  2  1
 2  1  1
 1  1  2

julia> Y = [2,3,3]
3-element Array{Int64,1}:
 2
 3
 3

julia> X = inv(A)*Y
3-element Array{Float64,1}:
 1.0
 2.220446049250313e-16
 0.9999999999999998

julia> round.(X) #四捨五入
3-element Array{Float64,1}:
 1.0
 0.0
 1.0

julia> A*X #確認
3-element Array{Float64,1}:
 2.0
 3.0 
 3.0

＊実習：大規模な連立一次方程式の求解シミュレーション

julia> N = 100; #この数を変えてみる！

julia> A = rand(0:9, (N,N)) #ランダムの正方形行列
100×100 Array{Int64,2}:
 5  7  5  5  9  3  5  2  5  9  4  1  7  3  8  0  1  4  5  7  5  …  6  5  9  4  0  2  1  3  1  2  7  9  2  9  4  0  9  6  5  7
 2  6  2  4  1  8  2  9  7  6  6  5  6  5  1  8  6  6  5  5  4     1  3  5  5  3  6  8  3  1  3  0  8  4  5  0  2  5  4  1  2
 1  1  2  1  1  8  9  3  5  9  8  0  4  0  9  7  6  3  4  9  8     3  8  6  5  3  1  8  9  0  1  2  0  2  6  5  0  7  4  1  6
 1  7  8  5  2  8  0  0  0  2  6  0  8  3  6  3  0  3  5  6  4     4  5  8  1  8  4  2  0  0  5  1  7  3  1  7  5  1  7  0  5
 5  8  9  4  4  7  6  4  4  5  1  1  4  6  3  9  7  3  4  8  7     4  0  2  4  9  7  1  6  1  0  9  8  5  0  3  8  4  7  5  5
 1  8  9  5  3  3  1  3  5  7  8  4  7  4  9  5  3  7  5  9  1  …  8  7  0  1  3  3  2  8  2  2  2  2  5  4  9  6  3  8  7  2
 ⋮              ⋮              ⋮              ⋮              ⋮  ⋱  ⋮              ⋮              ⋮              ⋮           
 8  9  1  3  3  9  6  2  3  5  3  3  6  6  6  5  5  4  4  7  8  …  6  5  4  2  8  5  9  1  5  6  3  3  7  9  3  5  0  5  3  5
 3  4  3  1  4  9  9  8  7  8  4  1  0  6  7  0  3  3  7  8  8     2  9  0  9  7  0  6  9  2  1  6  2  7  1  3  1  8  4  4  0
 9  6  8  3  8  5  3  7  8  0  6  9  1  9  5  0  4  1  3  7  6     5  8  3  6  3  7  7  4  3  8  5  3  8  6  2  2  8  4  9  1
 4  8  5  4  5  6  6  7  2  7  5  0  6  1  0  5  0  4  0  2  3     8  5  1  8  7  2  9  5  0  0  2  4  3  5  1  4  5  0  4  2
 9  6  5  8  3  9  6  7  5  3  4  5  0  8  0  6  2  2  0  3  3     4  7  4  5  4  2  8  1  4  5  4  5  4  3  4  5  2  4  7  0

julia> Xo = rand(0:9, N) #「答え」は ランダムの整数列とする。
100-element Array{Int64,1}:
 1
 2
 5
 2
 7
 7
 ⋮
 1
 3
 8
 8
 5

julia> Y = A*Xo #用意した「答え」を使って、Y 行列を計算
100-element Array{Int64,1}:
 2081
 1970
 2288
 1876
 2135
 2037
    ⋮
 1960
 1911
 2111
 1827
 1847

julia> X = inv(A)*Y #これが本番。連立一次方程式を解く
100-element Array{Float64,1}:
 1.0000000000000107
 2.000000000000341
 5.000000000000256
 2.0000000000004547
 6.999999999999801
 7.0000000000001705
 ⋮
 0.9999999999999432
 3.0000000000001705
 8.00000000000017
 8.00000000000017
 4.999999999999545

julia> 二乗和誤差 = sum(X.^2 - Xo.^2) #「答えと比較する」
1.771205404566187e-11

11. Linear Transformation 線形写像

• 線形変換とも呼ばれる。

• 詳しい説明はこちら (wikipedia)

• 入力が u, 変換行列が T, 出力が v とする。

\[ \mathbf{v}= \mathbf{Tu}\]

\[\begin{bmatrix}~\\出力\\(m \times p)\\~\end{bmatrix} = \begin{bmatrix}\mathrm{Transformation}\\\mathrm{Matrix}\\変換行列\\(m \times m)\end{bmatrix}\begin{bmatrix}~\\入力\\(m \times p)\\~\end{bmatrix} \]

平面 (2×2)の線形変換行列の例：

\[\begin{matrix} \theta~\mathrm{rad}回転\\\begin{bmatrix}\cos{\theta} & -\sin{\theta}& \\\sin{\theta} & \cos{\theta}\end{bmatrix}\end{matrix}~~~~~~\begin{matrix} 90 度回転\\\begin{bmatrix}0 & -1\\1 & 0\end{bmatrix}\end{matrix}~~~~~~\begin{matrix} x軸反転\\\begin{bmatrix}1 & 0\\0 & -1\end{bmatrix}\end{matrix}~~~~~~\begin{matrix} y軸反転\\\begin{bmatrix}-1 & 0\\0 & 1\end{bmatrix}\end{matrix}\]

練習：一点の線形写像を行う

\[\begin{bmatrix}v_1 \\ v_2\end{bmatrix} = \begin{bmatrix} (2\times2)\\変換行列 \end{bmatrix}\begin{bmatrix}u_1 \\ u_2\end{bmatrix}\]

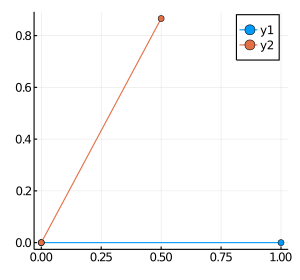
julia> T(t) = [  cos(t) -sin(t);
sin(t) cos(t)] #変換行列関数を定義

julia> u = [1;0]
2-element Array{Int64,1}:
 1
 0

julia> v = T(pi*60/180) * u # 60度回転
2-element Array{Float64,1}:
 0.5000000000000001
 0.8660254037844386

julia>  plot( size = (300,280)) #グラフ画面のサイズを指定

julia> plot!([0, u[1]], [0, u[2]],marker = 4)

julia> plot!([0, v[1]], [0, v[2]],marker = 4)

練習：複数点の線形写像を一気に行う

\[\begin{bmatrix}v_{11} & \cdots & v_{1n}\\ v_{21} & \cdots & v_{2n}\end{bmatrix} = \begin{bmatrix} (2\times2)\\変換行列 \end{bmatrix}\begin{bmatrix}u_{11} & \cdots & u_{1n}\\ u_{21} & \cdots & u_{2n}\end{bmatrix}\]

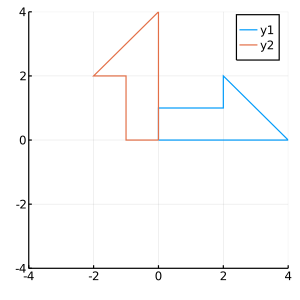
julia> u = [0 4 2 2 0 0; #矢印の頂点を定義
            0 0 2 1 1 0]
2×6 Array{Int64,2}:
0  4  2  2  0  0
0  0  2  1  1  0

julia> v = T(pi/2) * u
2×6 Array{Float64,2}:
 0.0  2.44929e-16  -2.0  -1.0  -1.0          0.0
 0.0  4.0           2.0   2.0   6.12323e-17  0.0

julia> plot(size=(300,300),xlims=(-4,4), ylims=(-4,4))

julia> plot!(u[1,:], u[2,:])

julia> plot!(v[1,:], v[2,:])

＊実習：線形写像

下記のようなグラフを転換行列で作成する。作成したグラフをワードに挿入する。

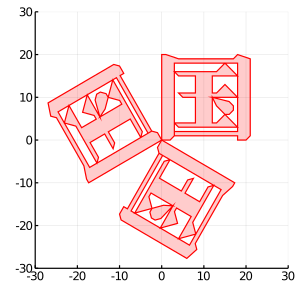
• 手順１：次の txt ファイルを開き、マウスで、頂点の数値データだけ選んでコピーする。

► kuni.txt

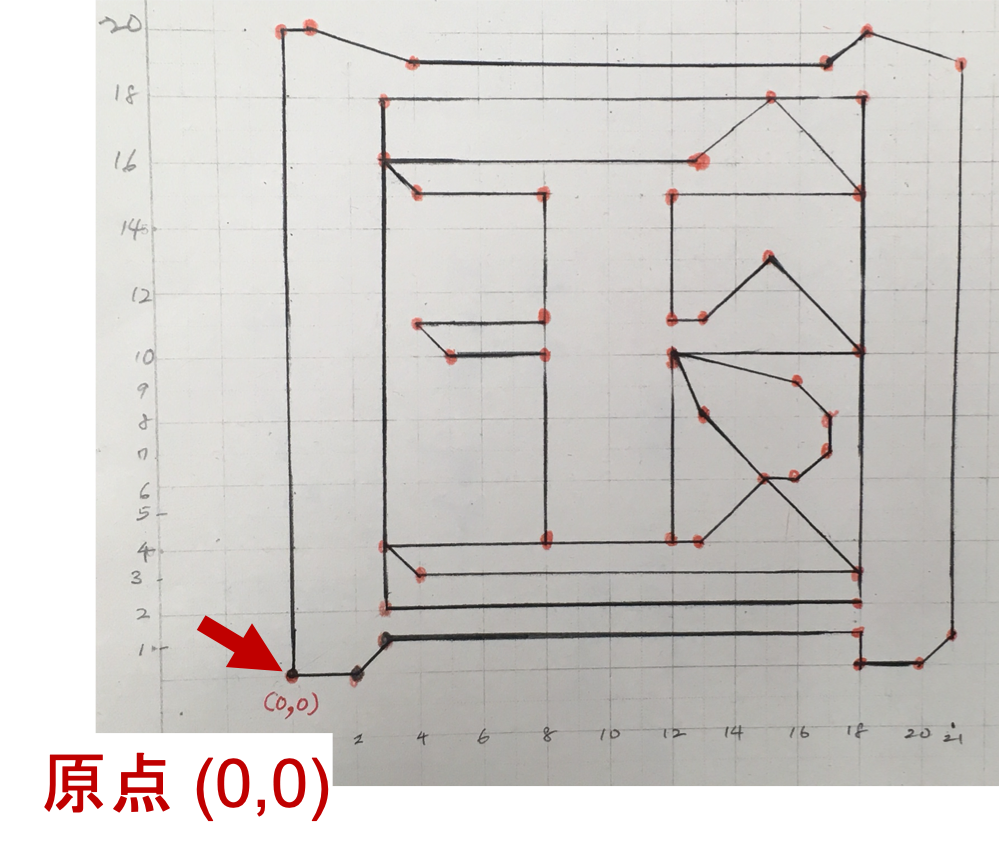
手順２：コピーしたデータで入力行列を作成：

julia> A = [#コピーしたデータをここに貼り付ける。
⋮    ⋮
8   4
3   4
3   1] #貼り付けったら、角括弧をつけてEnter


julia> A
51×2 Array{Int64,2}:
  3  1
 18  1
  ⋮  
  3  4
  3  1

• 手順３：作成した A は(51 × 2) の行列です。

• A 行列を (2 × 51) の行列に転置する。

julia> A = ❓
2×51 Transpose{Int64,Array{Int64,2}}:
 3  18  18  20  21  21  …
 1   1   0   0   1  19  …

• 手順４：新しい頂点の B と C 行列 (2 × 51) を転換行列で作成する。

julia>  B = ❓ * A
2×51 Array{Float64,2}:
 …
 …
  

julia> C = ❓ * A
2×51 Array{Float64,2}:
 …
 …

• 手順５：グラフ画面のサイズとグラフの範囲を指定する。色を変えて見てください。

• 下記の 0.2 という数字は塗りつぶしの　透明度です。

julia> plot(size = (300,300), xlims = (-30,30), ylims = (-30, 30), legend = false)

julia> plot!(A[❓], A[❓], fill = (0, 0.2,"red"), linecolor = "red")

julia> plot!(B[❓], B[❓], fill = (0, 0.2,"red"), linecolor = "red")

julia> plot!(C[❓], C[❓], fill = (0, 0.2,"red"), linecolor = "red")