データサイエンス CDS009 (チェン leechuin@yamanashi.ac.jp)　更新日: 2022-10-01

統計学入門 II：確率＆正規分布

今回の実習課題：

• 書いたコード、出力画面とグラフを１つの　word (.docx)にまとめて提出してください。

次の Julia パケージを使います：

► DataFrames 表データの取り扱い

► CSV テキストファイルをDataFrameに読み込む

► Plots グラフの作成

► Statistics 平均値、標本標準偏差、相関係数など

► Random ランダムの乱数

各自のプログラムの最初の所に下記のコードを挿入する。

using DataFrames
using CSV
using Plots
using Statistics
using Random

1. ランダムの乱数列

予想できない数列

復習：rand

例１：

julia> rand() #0から1までの浮遊小数点乱数
0.35847825435610314

julia> rand(1:4) #1から4までランダムの整数
1

julia> rand(1:4, 5, 3) #２次元乱数列
5×3 Matrix{Int64}:
 4  1  4
 1  4  4
 1  1  3
 2  2  1
 3  1  4

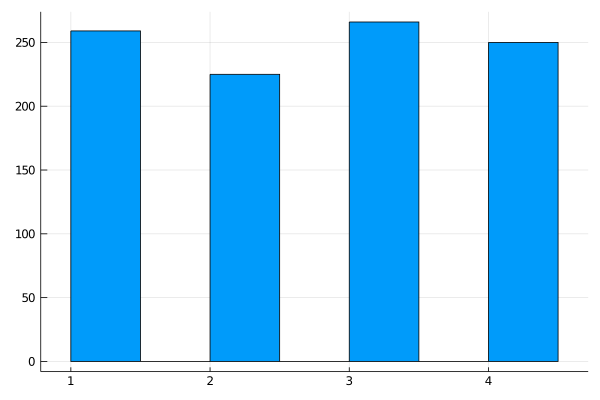
練習：rand の確率分布

例：連続一様分布

julia> histogram(rand(1:4, 1000), legend = false)

\[各整数が現れる確率 = \frac{1}{4}\]

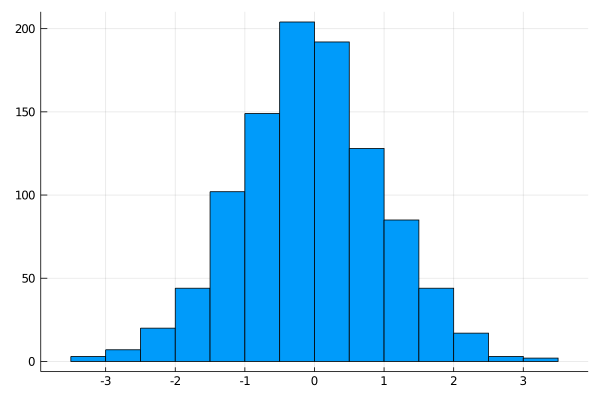
練習：randn 標準正規分布

標準正規分布の関数こちら：

\[ f(x) = \frac{1}{\sqrt{2 \pi}} \exp(-\frac{x^2}{2}) \]

• 平均値 = 0

• 標準偏差 = 1

例１：

julia> randn(5) #標準正規分布の乱数列
5-element Array{Float64,1}:
  0.25119996643007225
 -0.7864218548144813
  0.3641389111143696
  0.6778334619372927
 -0.5929366244376282

例２：

julia> histogram(randn(1000), legend = false)

2. 確率とモンテカルロ法

• 確率は事象の起こりやすさを定量的に示すもの。

• 英: Monte Carlo method とは乱数を用いて行うシミュレーション手法。

サイコロ Dice

• 六面がある。

• 一回投げた場合、可能な結果は 6個があるので各可能性の確率は 1/6

• ２回投げた場合、可能な結果は

(1,1)   (1,2)   (1,3)   (1,4)   (1,5)   (1,6)
(2,1)   (2,2)   (2,3)   (2,4)   (2,5)   (2,6)
(3,1)   (3,2)   (3,3)   (3,4)   (3,5)   (3,6)
(4,1)   (4,2)   (4,3)   (4,4)   (4,5)   (4,6)
(5,1)   (5,2)   (5,3)   (5,4)   (5,5)   (5,6)
(6,1)   (6,2)   (6,3)   (6,4)   (6,5)   (6,6)

► 可能性の数は 6×6 = 36個。

► 各可能性の確率は 1/36

3. 階乗 & 組み合わせの数

練習：階乗 Factorial

\[n! = 1\times 2 \times \dots \times (n-1) \times n\]

但し

\[0! = 1\]

例

\[1! = 1\]

\[2! = 1\times 2 = 2\]

\[5! = 1\times 2 \times 3 \times 4 \times 5 = 120\]

Julia の内部関数 factorialで\( 5!\)を計算する。

julia> factorial(5)
120

階乗 Factorialの応用例

[ A, B, C ] の並べ方：

    [ A, B, C ]
    [ A, C, B ]

    [ B, A, C ]
    [ B, C, A ]

    [ C, A, B ]
    [ C, B, A ]

[ A, B, C ] の並べ方の数は：

\[1\times 2 \times 3 = 3! = 6\]

＊実習課題１a：

[ A, B, C, D ,E, F ] の並べ方の数はいくつですか

julia> ABCDEF の並べ方の数 = factorial(❓)

練習：組み合わせの数 Combination

• 組み合わせの順次がない。

• n 個のものから r 個とる組み合わせの数は

\[_nC_r = \frac{n!}{r!(n-r)!} \]

である。

nCr　は二項係数 binomial coefficient と呼ばれる。

• ６個のカードから２個とる組み合わせは

        (1,2)   (1,3)   (1,4)   (1,5)   (1,6)
                (2,3)   (2,4)   (2,5)   (2,6)
                        (3,4)   (3,5)   (3,6)
                                (4,5)   (4,6)
                                        (5,6)

Julia の内部関数 binomialで\( _6C_2 \)を計算する。

julia> binomial(6,2)
15

4. 乱数列の例：ロト６

• １から４３までの４３個の数字の中から異なる６個を選択するものである。

• 数字の重複がない。

＊実習課題１b：ロト６の当選確率

本数字６個と全て一致する当せん確率 = 1/6,096,454

Julia でこの数字を算出する。

julia> 組み合わせの数 = binomial(❓,❓)
6096454

julia> 当選確率 = 1/binomial(❓,❓)
1.6402977862213017e-7

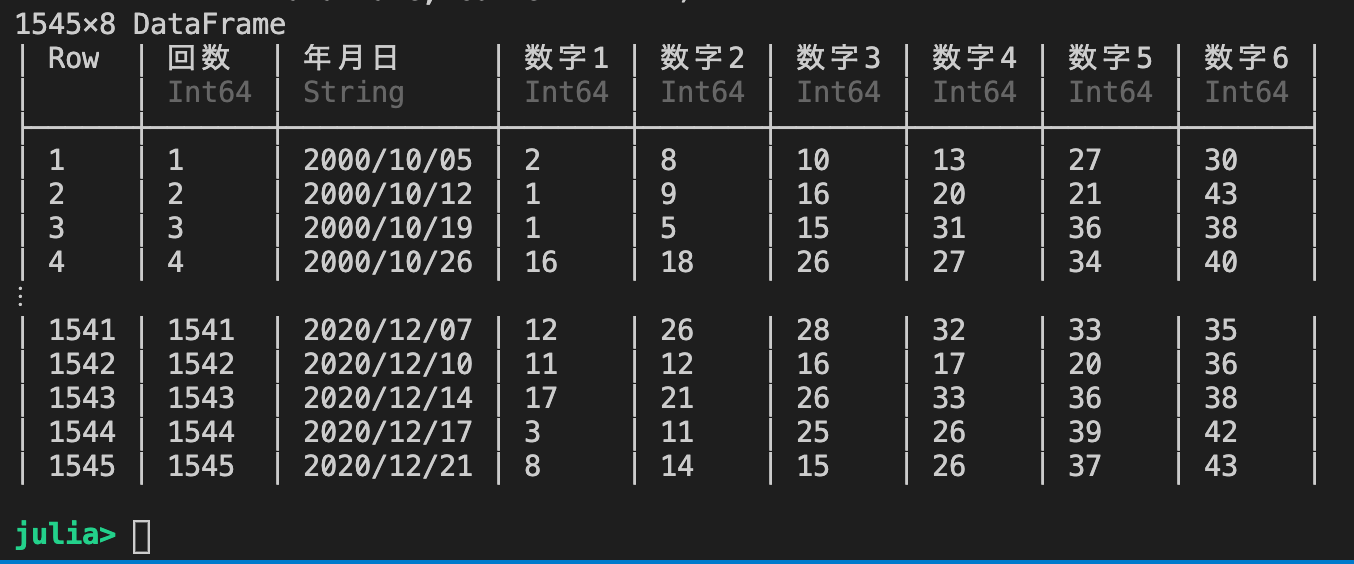
＊実習課題１c：ロト６の過去の抽選数字データ

過去の抽選数値データ(2000年から2020年まで)を「名前をつけ保存」で Julia の作業スペースに保存する。

ファイルはこちら：Loto6data.txt

下記のコードを順次に実行する。

Y = CSV.read("Loto6data.txt", DataFrame, comment = "#")

出力

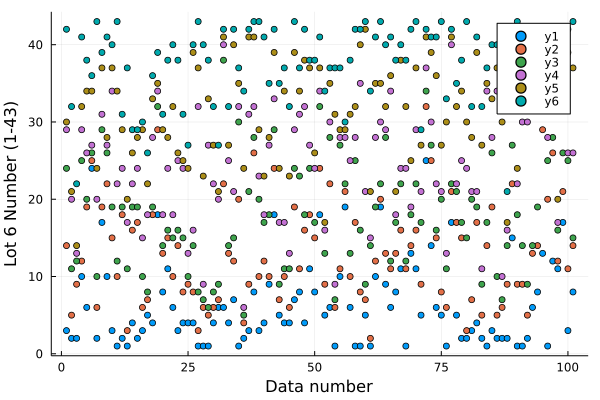
#直近１００回のデータを用いて散乱図を作成
N = 100
scatter( Y.数字1[end-N:end])
scatter!(Y.数字2[end-N:end])
scatter!(Y.数字3[end-N:end])
scatter!(Y.数字4[end-N:end])
scatter!(Y.数字5[end-N:end])
scatter!(Y.数字6[end-N:end])
scatter!(xlabel = "Data number", ylabel = "Lot 6 Number (1-43)")

各数字が現れる頻度

全数字列 = []
append!(全数字列, Y.数字1)
append!(全数字列, Y.数字2)
append!(全数字列, Y.数字3)
append!(全数字列, Y.数字4)
append!(全数字列, Y.数字5)
append!(全数字列, Y.数字6)
histogram(全数字列, bins=1:43, legend = false)
histogram!(xlabel = "Lot 6 number", ylabel = "Frequency")

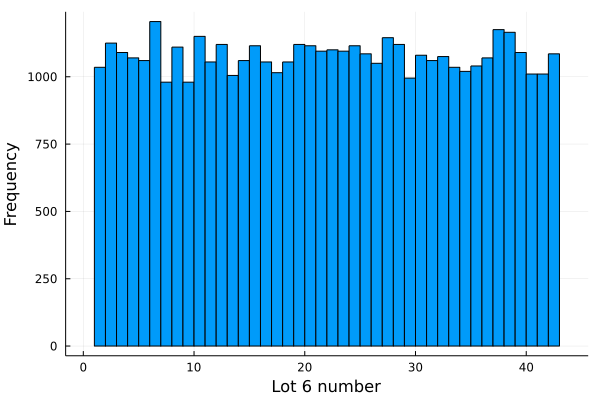
＊実習課題１d：抽せん数字の合計値

ロト６の抽選数字の和はどうなるか分析してみる。

数字合計列 = Y.数字1 + Y.数字2 + Y.数字3 + Y.数字4 + Y.数字5 + Y.数字6
println("分析結果：")
println("データの数 = ", length(数字合計列))
println("合計値の平均 = ", mean(数字合計列))
histogram(数字合計列, legend = false, xlabel = ❓)

分析結果：
データの数 = 1545
合計値の平均 = 131.97346278317153

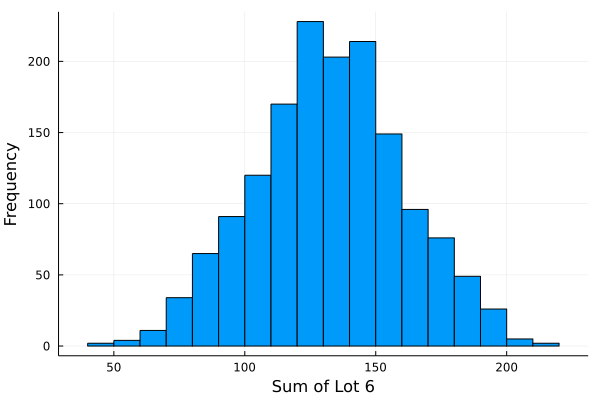
＊課題質問：合計値は予想ができますか ?

• 次の比較とシミュレーションを参考してこの現象について論じてください。

• 注意：ロート６の数字列の予測は決してできません。

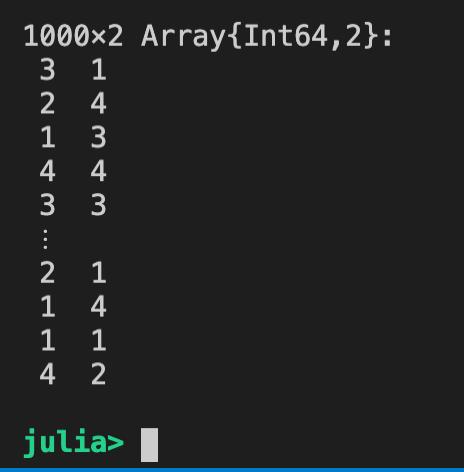
解説：簡易ロト２

１番から４番の乱数2組。数字の重複あり。

#簡易ロート２
A = rand(1:4, 1000,2)
display(A)
s = sum(A, dims = 2) #
histogram(s, legend = false, size=(400,300))

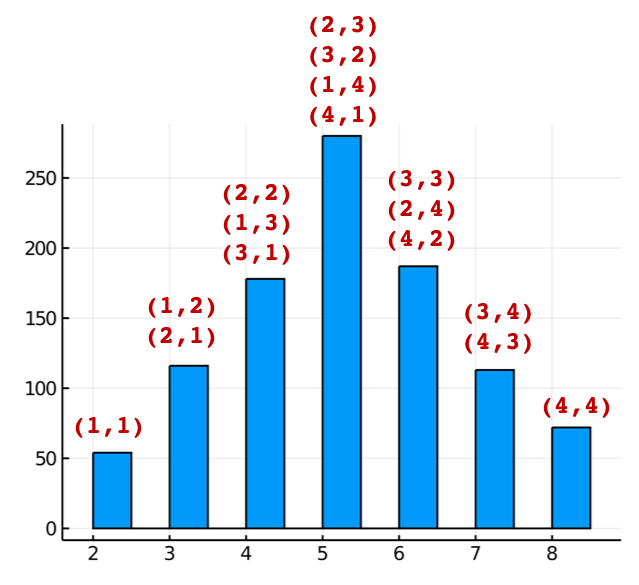
＊チャレンジ：ロト６のシミュレーションと合計値の分析

#ロト６の数字組み合わせを作成する自作関数
function 抽選()
    Numbers = Array(1:43)
    数字列 = []
    for i in 0:5
        ランダム位置 = rand(1:43 -i)
        push!(数字列,  Numbers[ランダム位置])#数字列に数字を追加する
        #選んだ数字をリストから削除
        deleteat!(Numbers,ランダム位置)
    end
    return 数字列
end

#確認用
println("ロト６の合計値シミュレーション")
println("数字の組み合わせの確認用。")
for i in 1:5
    println(抽選())
end

#ここから分析の本番
#理想は６００万回以上ですがパソコンの負荷を考慮しないと。
N = 100000 
数字合計列 = [] 
for i in 1:N
    X = 抽選()
    push!(数字合計列, sum(X))
end
println("\nシミュレーション結果：")
println("合計の平均値 = ", mean(数字合計列))
println("単純理論値 = ", (sum(1:6) + sum(38:43))/2)
histogram(数字合計列, legend = false)

出力：

ロト６の合計値シミュレーション
数字の組み合わせの確認用。
Any[7, 1, 6, 2, 37, 30]
Any[31, 19, 14, 20, 15, 25]
Any[31, 15, 14, 28, 29, 18]
Any[42, 30, 11, 32, 29, 34]
Any[39, 10, 25, 29, 30, 16]

シミュレーション結果：
合計の平均値 = 131.93751
単純理論値 = 132.0

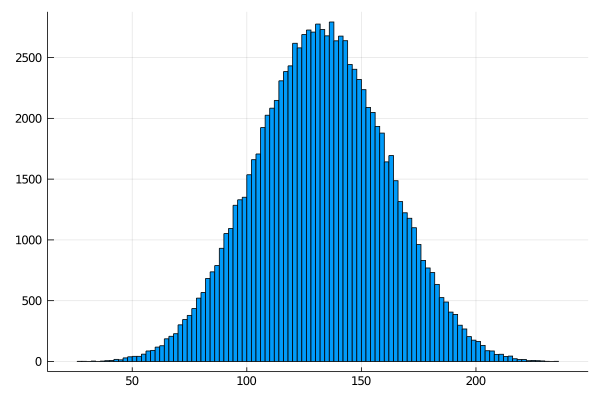
• 抽選の回数 N が大きい時には、乱数の和はほぼ「正規分布」に従って分布する。

• 正規分布が現れることは不思議的な結果ですが、それを中心極限定理 central limit theorem という。

5. 内部関数： findall()

• 検索条件に満たした要素を検索する。

文法：

findall(x->  検索条件, 入力配列)

例：

julia> a = [10, 20, 30, 40, 50]
5-element Array{Int64,1}:
 10
 20
 30
 40
 50

julia> findall(x-> x==30, a)
 1-element Array{Int64,1}:
3

julia> findall(x-> x>30, a) #30より大きい要素を検索
2-element Array{Int64,1}:
4
5

julia> findall(x-> x<30, a) #30より小さい要素を検索
2-element Array{Int64,1}:
1
2

julia> length( findall(x-> x>20, a) ) #20以上の要素の「数」
3

6. 確率で pi を求める

• 円周率を算出するのはいろいろな方法があります。

• 効率はそんなによくないが、ランダムの射的を用いて、円周率を算出することもできる。

方法：

• 次のように円形が描いてある正方形の的にランダムで当てる。

• 円形に入った数を入ってない数で円周率を計算する。

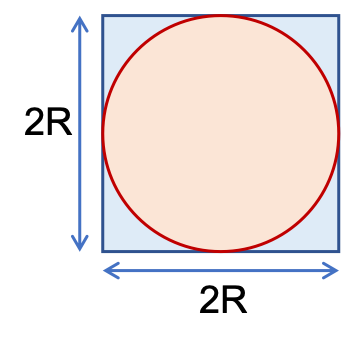
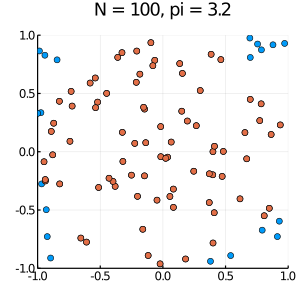
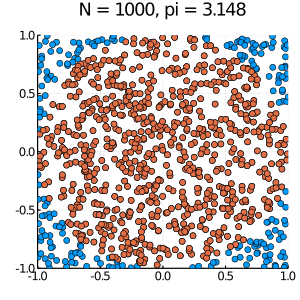
＊実習課題２：rand で pi を求める

下記のコードを実施する。次の式を導いて、なぜ piを確率で算出できるか説明してください。

\[ \pi = \frac{4*命中数}{N}\]

N = 5000　#この数を変えてみてください
R = 1 #円の半径
x = rand(-R: 0.000001: R, N) #ランダムの x
y = rand(-R: 0.000001: R, N) #ランダムの x
r = sqrt.( x.^2 + y.^2 ) #中心から 点 までの距離
命中 = findall(p-> p<=R, r) #半径 R 以内にある 点 を見つける。
命中数 =  length(命中)
println("ランダムの射的で、円周率を求める")
println("当てる回数 N = ", N)
println("確率で算出した π = ", 命中数 * 4/N) #この式を導く
println("教科書に載っている π = ", 3.14159265)
println("")
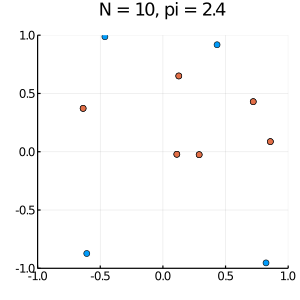
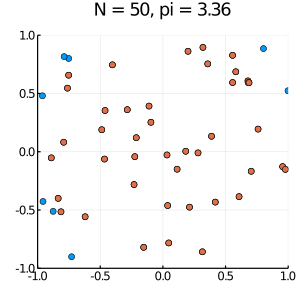
scatter(x,y, size = (300,300), legend=false)
scatter!(x[命中],y[命中], size = (300,300))

7. 正規分布　Normal Distribution

► ガウス分布（Gaussian distribution）とも呼ばれる。

► 連続的な変数に関する確率分布の一つ。

\[ f(x) = \frac{1}{\sigma\sqrt{2 \pi}} \exp \left[ -\frac{1}{2} \left( \frac{x-\mu}{\sigma} \right)^2 \right] \]

\[ \mu = 平均値 \]

\[ \sigma = 標準偏差 \]

\[\int_{-\infty}^{\infty} f(x) dx = 1 \]

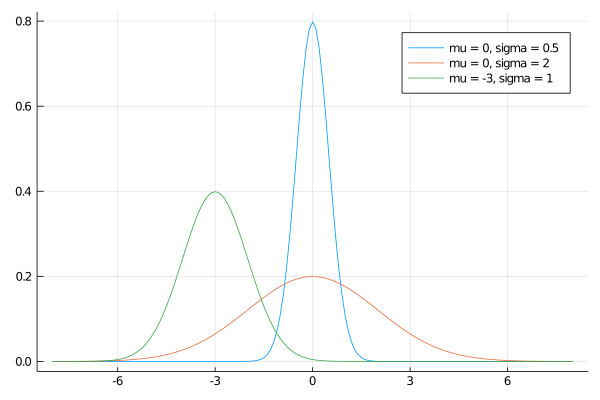
練習：正規分布をプロットする

f(x, mu, sigma) = (1/(sigma*sqrt(2*pi))) * exp(-((x-mu)/sigma)^2/2)
x = -8:0.1:8
plot(x, f.(x, 0, 0.5), label = "mu = 0, sigma = 0.5")
plot!(x, f.(x, 0, 2), label = "mu = 0, sigma = 2")
plot!(x, f.(x, -3, 1), label = "mu = -3, sigma = 1")

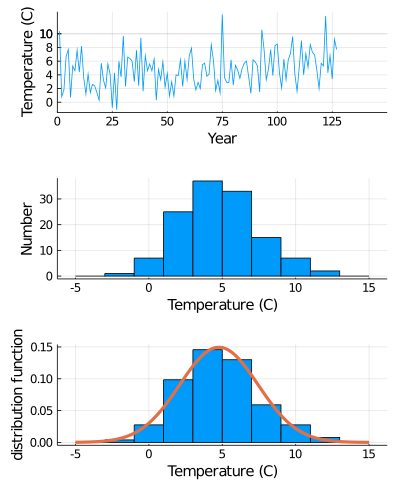
8. 正規分布の例

＊実習課題３a：甲府１２月１１日の日平均気温

• 気象庁から1894年からの気温データが入手できる。

• 「甲府１２月１１日の日平均気温」はこちら：

Kofu_TemperatureOn11Dec.txt


A = CSV.read("Kofu_TemperatureOn11Dec.txt", 
    DataFrame, comment = "#")

mu = mean(A.気温)
println("平均値 mu = ", mu)

sigma = std(A.気温)
println("標準偏差 sigma= ", sigma)

O = plot(A.気温, 
    xlabel = "Year", 
    ylabel = "Temperature (C)",
    xlims =(0,150))
P = histogram(A.気温, 
    bins=-5:2:15,
    xlabel = "Temperature (C)", 
    ylabel = "Number",
    )
Q = histogram(A.気温, 
        bins=-5:2:15,
        xlabel = "Temperature (C)", 
        normed = true,
        ylabel = "distribution function"
        )
#正規分布モデルを立てる
f(x) = (1/(sqrt(2*pi)*sigma)) * exp(-((x-mu)/sigma)^2/2)
x = -5:0.01:15
plot!(x, f.(x), linewidth = 3)

#グラフをまとめる
plot(O, P, Q, layout = (3,1), 
    legend = false, 
    size=(400,500),
    labelfontsize = 10)

9. 確率分布関数から確率と任意の期待値（平均値）を求める

確率の計算

\[確率分布関数~=~f(x)\]

\[ 確率 P(a\le x \le b) = \int_a^b f(x) dx\]

数値計算の場合

\[ 確率 P(a\le x \le b) \approx \sum_{i=1}^{N} f(x_i) \Delta x\]

期待値・平均値の計算

x の平均値

\[ \langle x \rangle = \int_{-\infty}^{\infty} x f(x) dx\]

x^2 の平均値

\[ \langle x^2 \rangle = \int_{-\infty}^{\infty} x^2 f(x) dx\]

任意の関数 g(x) の平均値

\[ \langle g(x) \rangle = \int_{-\infty}^{\infty} g(x) f(x) dx\]

数値計算の場合

\[ \langle x \rangle \approx \sum_{i=1}^{N} x_i f(x_i) \Delta x\]

\[ \langle x^2 \rangle \approx \sum_{i=1}^{N} x_i^2 f(x_i) \Delta x\]

\[ \langle g(x) \rangle \approx \sum_{i=1}^{N} g(x_i) f(x_i) \Delta x\]

＊実習課題３b：正規分布関数から確率を求める

正規分布関数と数値積分の方法で下記の確率を算出する。

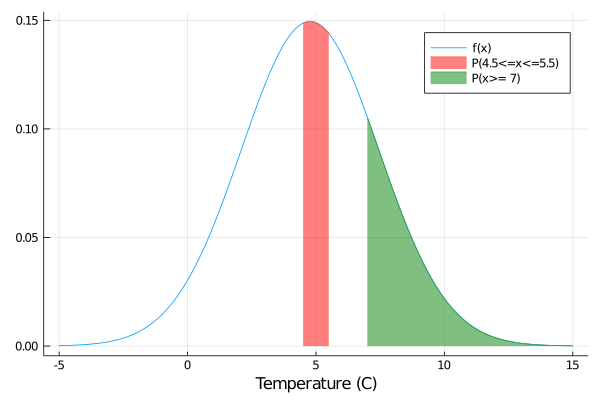
問１：甲府の12月１１日の気温が 5 度＋/- 0.5 の確率

問２：甲府の12月１１日の気温が 7 度以上の確率

下記のコードを完成させ。

println("----")
println("正規分布関数と数値積分で確率を求める")
f(x) = (1/(sqrt(2*pi)*sigma)) * exp(-((x-mu)/sigma)^2/2)
x = -5:0.01:15
plot(x, f.(x), label = "f(x)", xlabel = "Temperature (C)")

x = 5-0.5 :0.01: 5 + 0.5
println("5 度＋/- 0.5 の確率　= ", sum(f.(x) * 0.01))
plot!(x, f.(x),fill = (0, 0.5,"red"), label = "P(4.5<=x<=5.5)")

x = ❓: 0.01: 15
println("7 度以上の確率　= ", sum(f.(x) * 0.01))
plot!(x, f.(x), fill = (0, 0.5,"green"), label = "P(x>= 7)")

出力：

平均値 mu = 4.77007874015748
標準偏差 sigma= 2.669650561540762
----
正規分布関数と数値積分で確率を求める
5 度＋/- 0.5 の確率　= 0.14948646029364848
7 度以上の確率　= 0.20224272162944604

出力グラフ：

＊実習課題３c：正規分布関数から平均値を求める