データサイエンス CDS009    (チェン leechuin@yamanashi.ac.jp)　更新日: 2022-10-01

---

プログラムの流れの制御＆関数

1. 統合開発環境 IDE (Integrated Development Development)

 • 詳細な説明は こちら (wikipedia)

 • 長いプログラムを書くときに、IDEを使うの効率的です。

 • 普通のメモ帳より、Syntax highlighting (構文着色)の機能が付いているので、文法ミスを防ぐことができる。

Visual Studio Code (VS Code)

 • Windows、Linux、macOS 用の無料IDEです。

 • 未インストールの方、下記のリンクから該当のファイルをダウンロードしてインストルしてください。

 • ダウンロードのリンクは こちら：https://code.visualstudio.com

Julia 用 Extension の追加

Visual Studio Code に Julia 用の構文着色などの機能が付いていない。

VS Code を開き、「Manage 管理」の Icon をクリックして「extensions」 を選んでください。

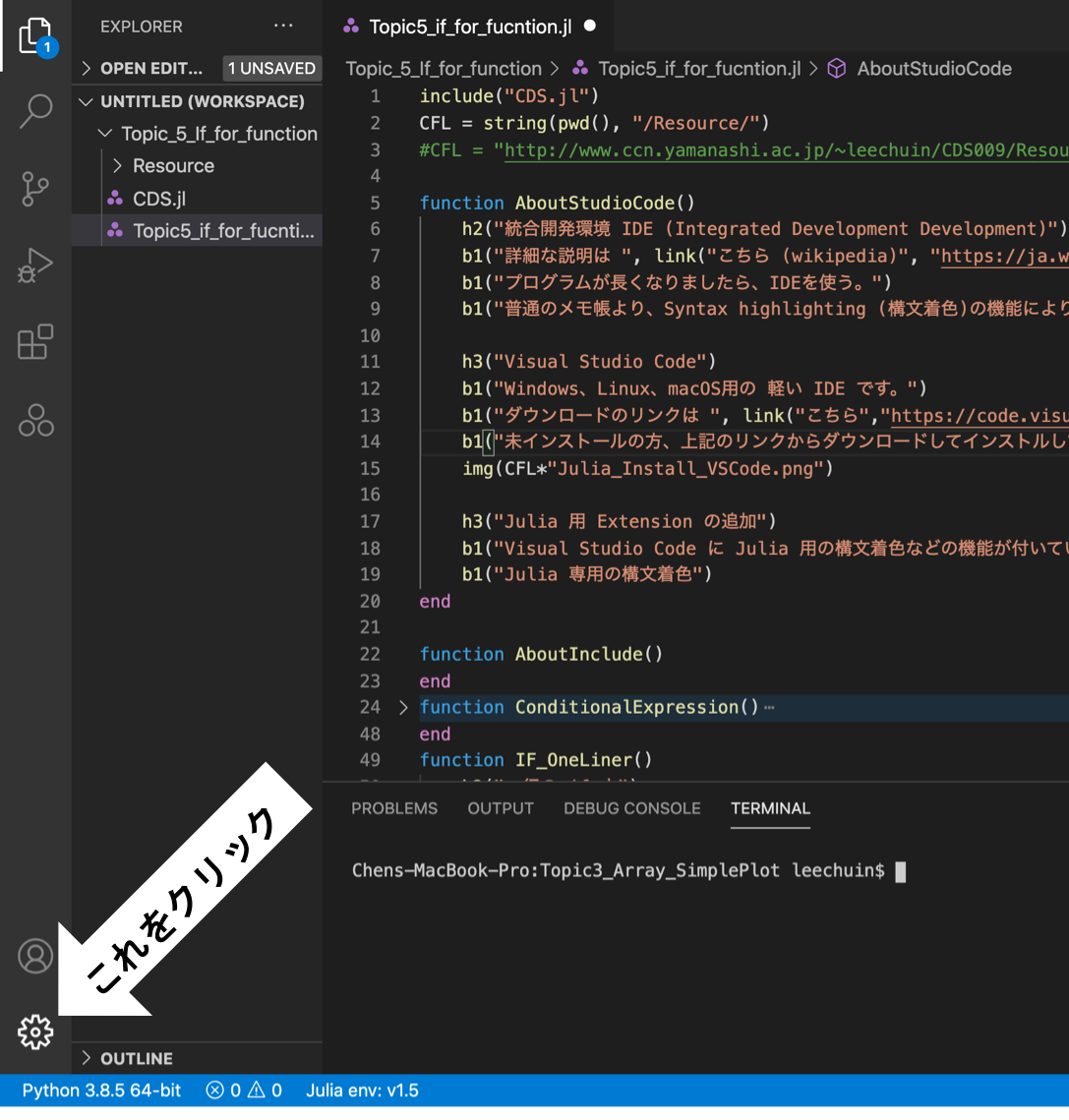
検索欄に 「 julia 」を入力する。Julia Language Support が出たら、それを選んでください。

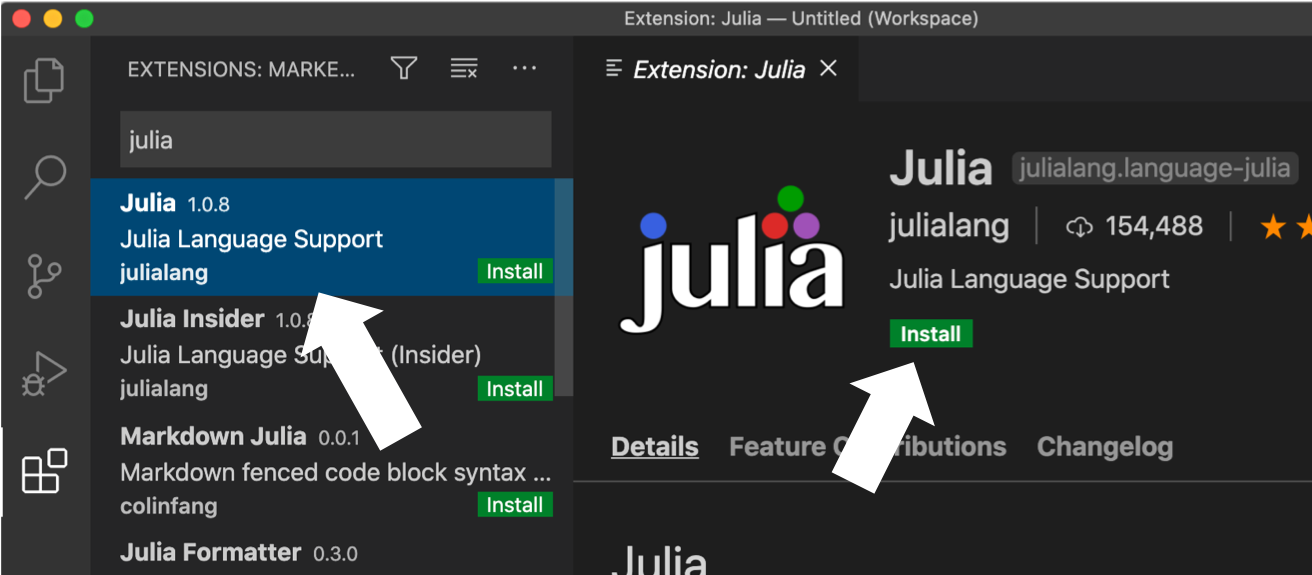
Test .jl ファイル

 • 今後のプログラムファイルを保管するフォルダーを作る。すでにありましたら、しなくても良い。

 • 「File」→「Open Folder」 で上記のフォルダーを指定する。

 • 「File」→「New File」で新規のファイルを開く

 • 簡単の指令を書き込む。例えばprint("hello")

 • ファイルを作業フォルダに保存する。

 • ファイル名の拡張子を .jl 例えば test.jl にしてください。

 • Juliaファイルであることが認識されたら、構文が着色される。

 • Alt-Enter を押したら、Julia が起動し、ファイルの内容が実行される。

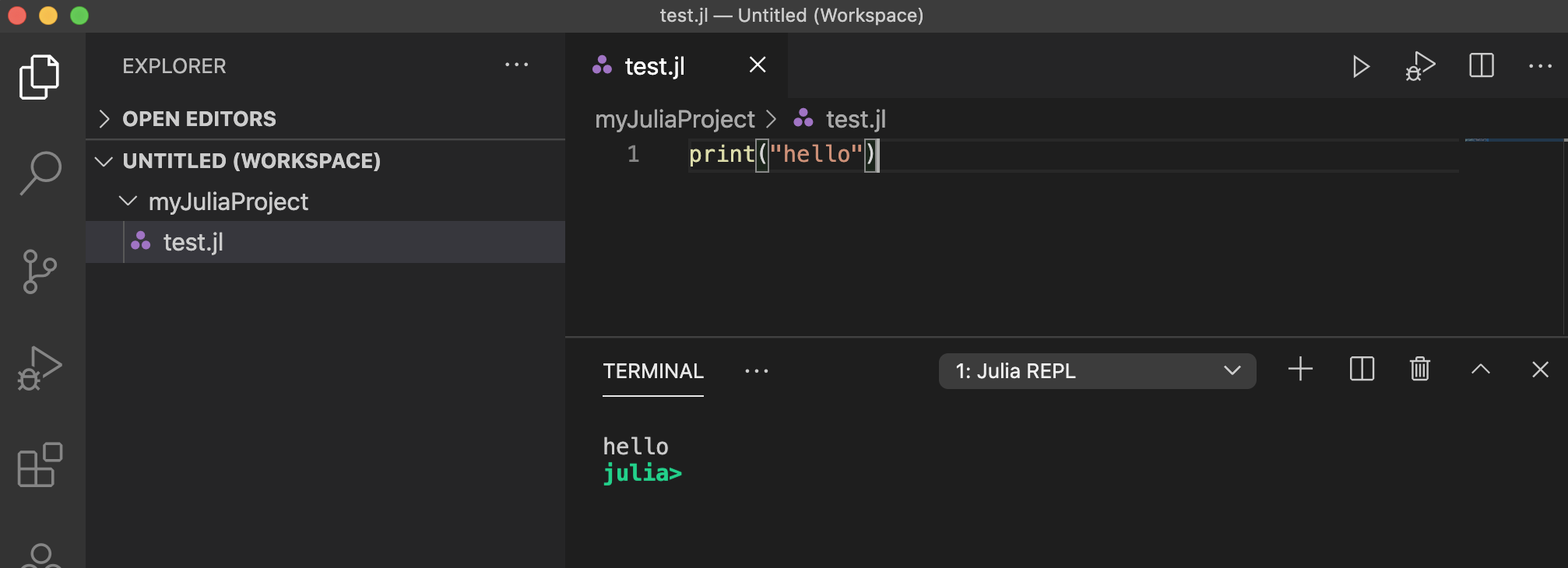
コードの実行方法

１）全部実行する： Alt-Enter を入力する。または次のブタンをクリックする。

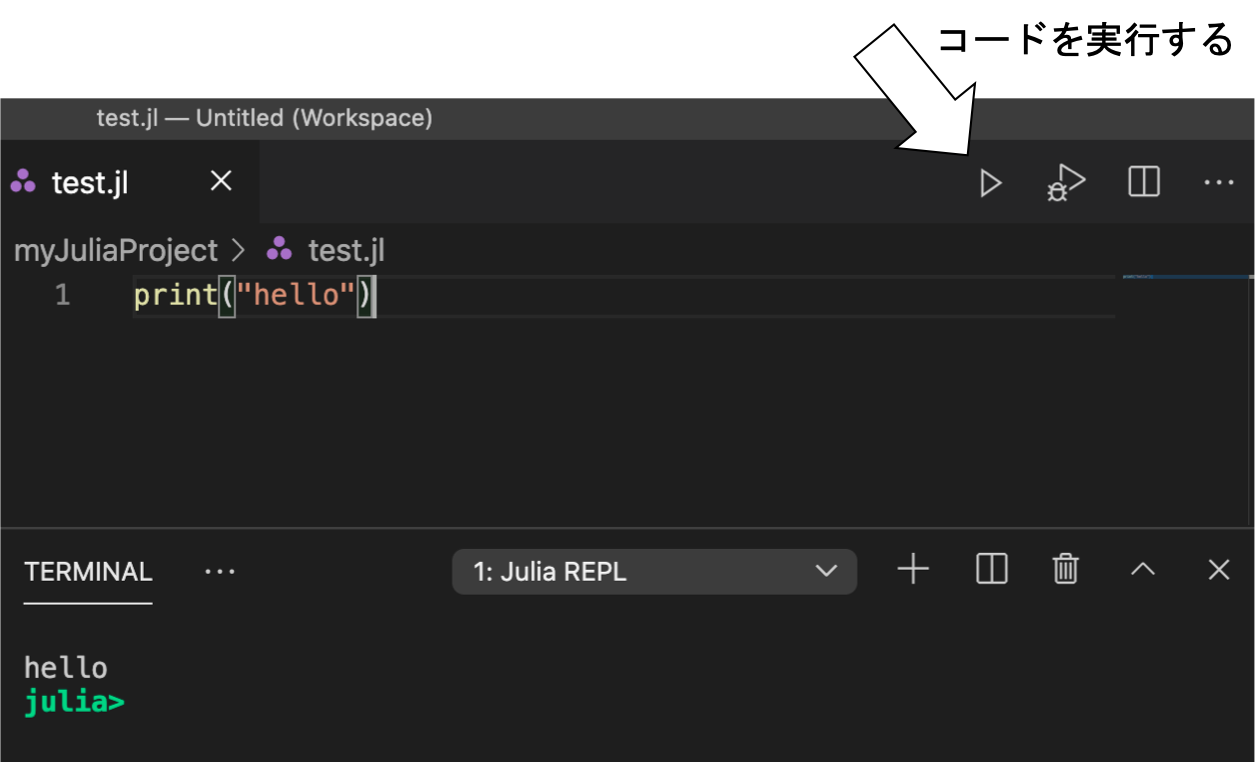
２）一部だけ実行する：

        ► 「マウス」、または「Shift-矢印キー」で実行したい部分を選ぶ。

        ► Control-Enter を入力。

        ► またはパネルの項目「Terminal」 → 「Run Selected Text」

        ► 注意点：一度 Control-Enter または Shift-Enter を入力して Julia のターミナルを起動する必要がある。

３）一行だけ実行する：

        ► 「マウス」または「矢印キー」でカーソルを目的まで動かす。

        ► Control-Enter を入力。

その他のShort Cut Key

https://www.julia-vscode.org/docs/dev/userguide/keyboard/

---

2. include と cd 関数

 • 下記はVS Codeの中でJuliaが起動出来ない、またはコードを実行できない場合の追加資料です。

 • その問題がなければ、この項目を飛ばしても良い。

Julia のデフォルト作業空間内で　ファイルを実行する

 • pwd() を使って作業空間を調べる。

 • pwd は　print working directory の省略です

 • Julia コードのファイルをその「作業空間」のフォルダー内に保存する。

 • include 関数で　ファイルを実行する。

julia> include("あなたのファイル名")

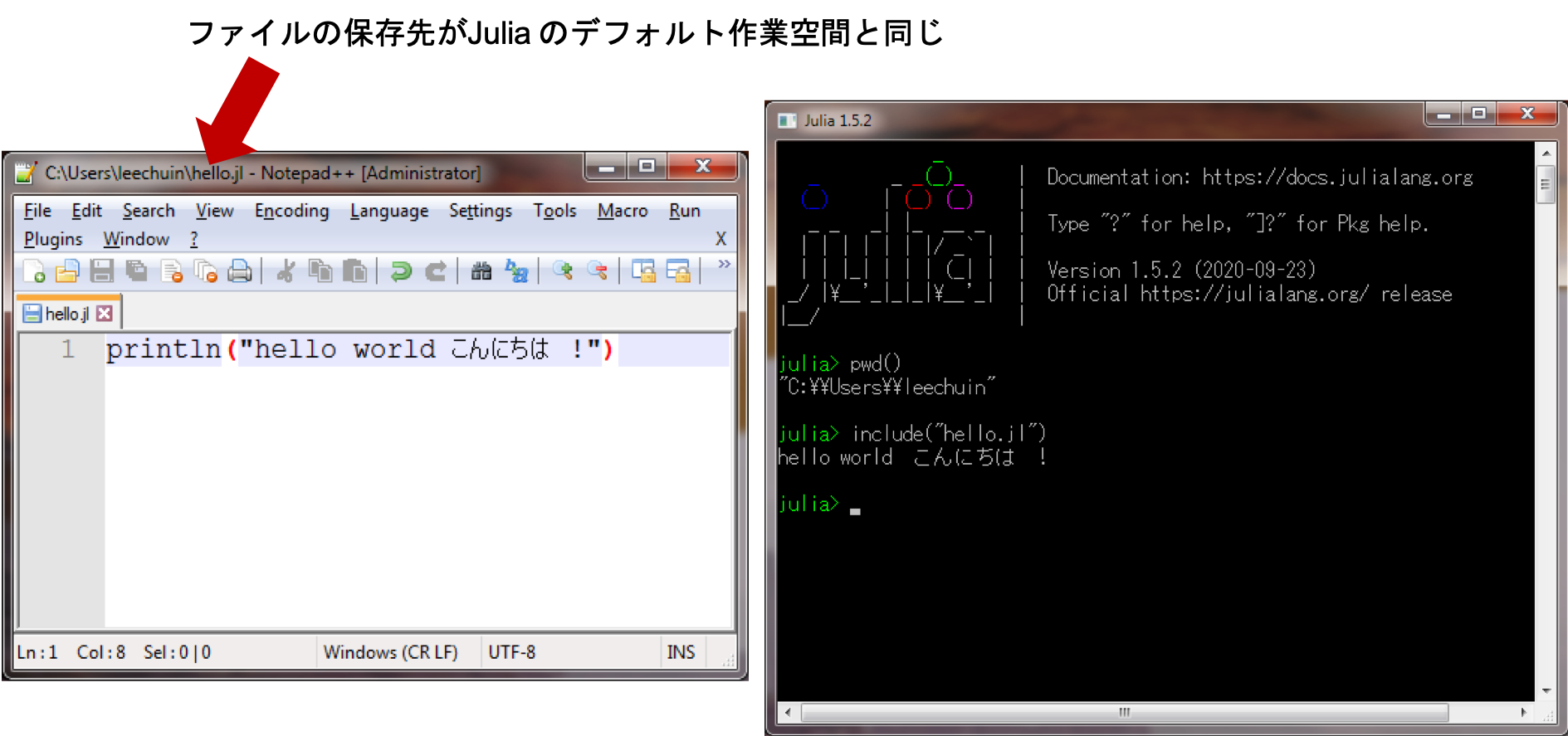
任意のデフォルトでファイルを実行する

 • cd 関数を使って作業空間の変更を行う。

 • cd は　change directory の省略です。

julia> cd("ファイルの保存先")

julia> pwd() #確認用。しなくても良い。

julia> include("あなたのファイル名")

---

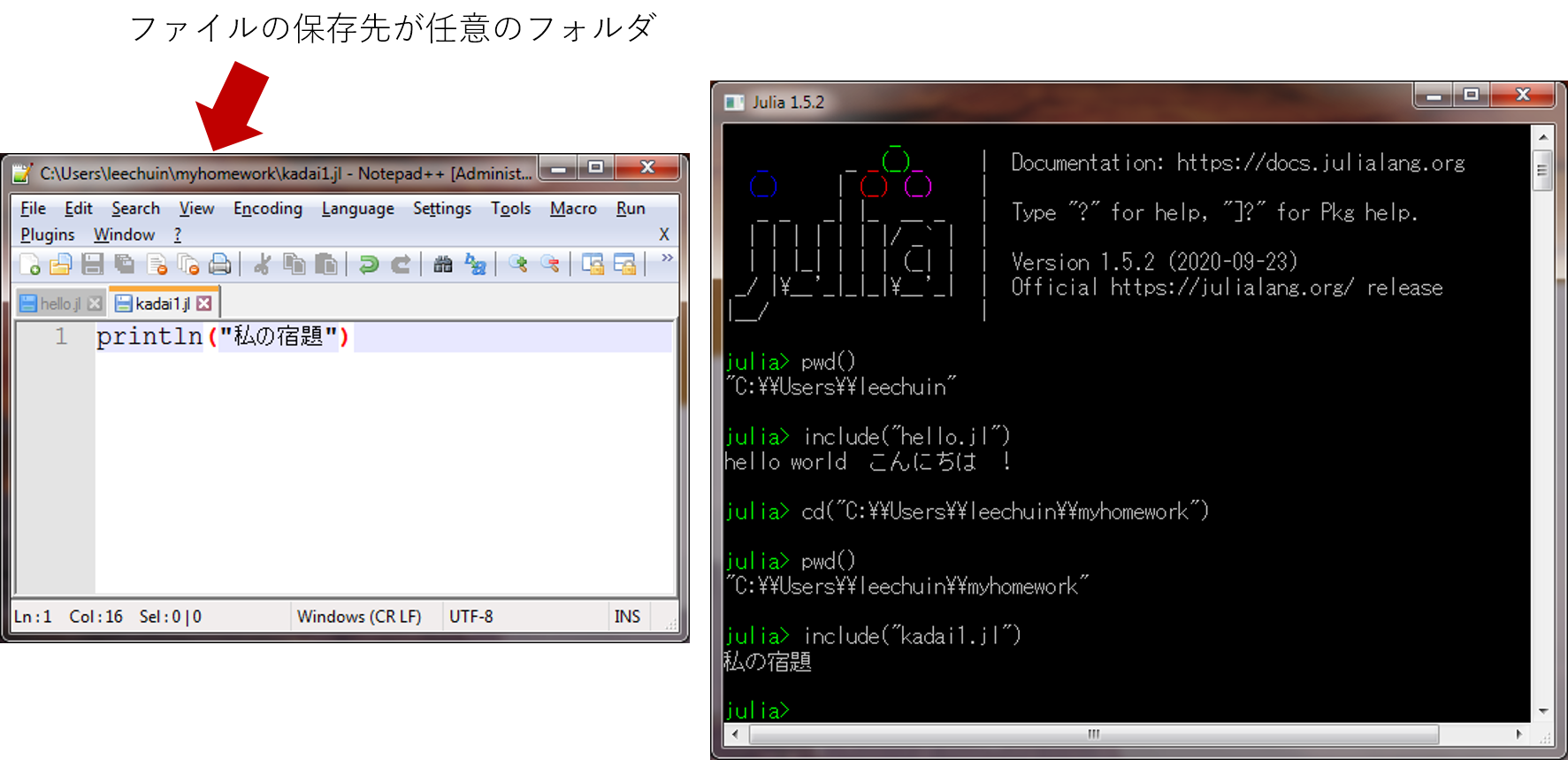
3. 条件式 Conditional Expression

 • 数式に似ているが、その結果が true 真 または false 偽 しかない。

 • つまり、条件式の型は Boolean ブリアンである。

\[ \begin{matrix}プログラミング &~ &数学\\\texttt{x > y} &~ &x > y & \\\texttt{x < y} &~ &x < y & \\\texttt{x >= y} &~ &x \geq y & \\\texttt{x <= y} &~ &x \leq y & \\\texttt{x == y} &~ &x = y & \\\texttt{x != y} &~ &x \neq y & \\\end{matrix}\]

例：

julia> x = 3; y = 4; z = 3;

julia> x > y
false

julia> x == z
true

julia> y != z
true

julia> x <= z
true

---

4. if-文：条件評価

Flow chart (if の流れ図)

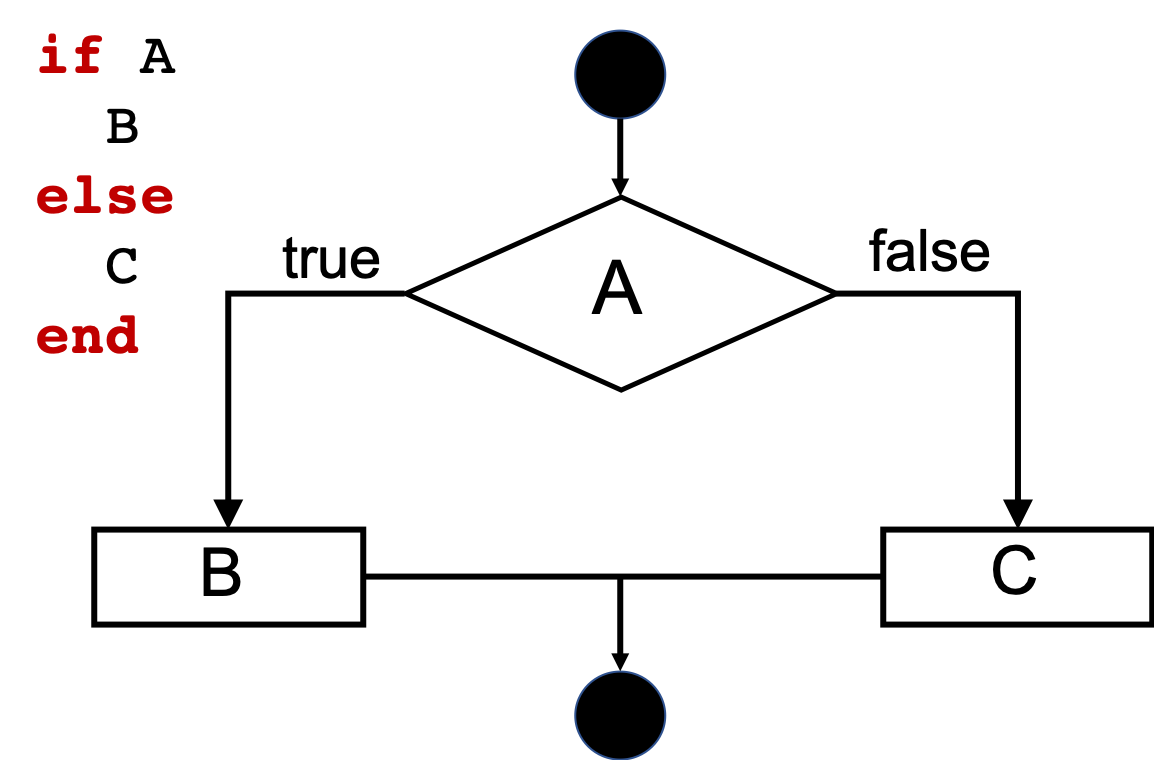
例：if - else - end

x = 2
y = 3
if x > y
    println("x は y より大きい。")
    z = 1
else
    println("x は y より小さいかもしれない。")
    z = -1
end
println("z = ", z)

x は y より小さいかもしれない。
z = -1

例：if - elseif - elseif - end

x = 2
y = 3
if x > y
    println("x は y より大きい。")
    z = 1
elseif x < y
    println("x は y より小さい。")
    z = -1
else
    println("その他。つまり x = y")
    z = 0
end
println("z = ", z)

x は y より小さい。
z = -1

---

5. 条件演算子(?:)

簡単の条件評価であらば、条件演算子 (?:) を使えば一行で実行できる。

条件式 ? 真の時の値 : 偽の時の値

julia> x = 3

julia> x > 3 ? "はい" : "違います"
"違います"

応用例

\[ \begin{align} f(x) &= x^2,~\mathrm{if}~x< 1\\&= 1,~~\mathrm{otherwise}\end{align}\]

julia> f(x) = x < 1 ? x^2 : 1
f (generic function with 1 method)

julia> t = Array(-1.5 :0.1: 1.5);

julia> plot(t, f.(t))

---

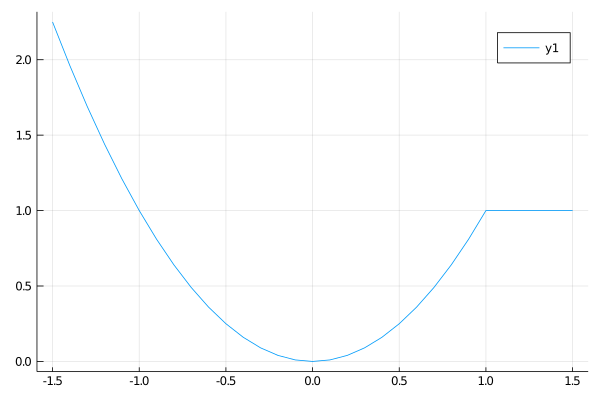
6. for-文

同じ処理を for のループ内に繰り返して実行することができる。

練習：同じ処理 N 回 行う

for x in 1:5
    print("これは ", x)
    print(" 回目です。\n")
end

これは 1 回目です。
これは 2 回目です。
これは 3 回目です。
これは 4 回目です。
これは 5 回目です。

練習：配列の要素を抽出して同じ処理を行う。

A = [12, 34, 56, 78]
for x in A
    println("要素 = ", x)
end

要素 = 12
要素 = 34
要素 = 56
要素 = 78

＊実習課題 1 ：ターミナルの表示制御

 • 下記プログラムを完成させ。

 • プログラムファイル .jl を提出してください。

 • ファイル名に課題番号を記入してください。

 • 出力画面を説明付きで Word に添付してください。

N = 6
println("これは例です")
for n in 1:N
    println("+"^n)
end

println("\nこれは実習課題です")
for ❓❓❓
    ❓❓❓　#hint:スペースを使う。
end

出力

これは例です
+
++
+++
++++
+++++
++++++

これは実習課題です
     +
    ++
   +++
  ++++
 +++++
++++++

hint

julia> println("+" * " "^3 * "+"^2)
+   ++

---

7. for-for文

 • for ループのなかで、 さらに for ループを実行する。

 • 「多重ループ」とも言われる。

 • ２次元 or ３次元配列の処理によく使われている。

練習：二重ループ

N = 1
println("- Start ---")
for i in 1:3
    for j in 1:2
        println("This is i = ", i, "	j = ", j , "	N = ", N)
        N += 1
    end
end
println("- End ---")

T- Start ---
This is i = 1   j = 1   N = 1
This is i = 1   j = 2   N = 2
This is i = 2   j = 1   N = 3
This is i = 2   j = 2   N = 4
This is i = 3   j = 1   N = 5
This is i = 3   j = 2   N = 6
- End ---

＊実習課題 2：行列の要素の抽出

 • 次のプログラムを完成させ。

 • プログラムファイル .jl を提出してください。

 • ファイル名に課題番号を記入してください。

 • 出力画面を説明付きで Word に添付してください。

A = rand(0:9, (3,4)) #ランダム整数の行列
println("行列を print で表示する")
println("A = ", A)

println("\n自己流で行列を表示する")
M = length(A[:,1]) # 行数
N = length(A[1,:]) # 列数
print("┌ " * " "^(N*2) * "┐\n")
for m in 1: M
    print("| ")
    for n in 1: N
        print(A[❓ , ❓])
        print("❓")
    end
    print("|\n")
end
print("└ " * ❓ * "┘\n")

行列を print で表示する
A = [7 2 4 0; 0 4 7 7; 7 3 4 2]

自己流で行列を表示する
┌         ┐
| 7 2 4 0 |
| 0 4 7 7 |
| 7 3 4 2 |
└         ┘

---

8. function-文：関数の定義

関数を定義するには最も標準的な書き方はこちら：

function 関数名(入力)
    計算・実行内容
    return 計算結果
end

例：

function myf(x, y)
    print("計算始め\n")
    Z = x^2 + y^2
    Z = sqrt(Z)
    return Z
end
print("結果：", myf(3, 4))

計算始め
結果：5.0

計算結果が関数ブロックの最終行であれば, return を書かなくても良い。

function myf(x, y)
    print("計算始め\n")
    Z = x^2 + y^2
    Z = sqrt(Z)
end

上記と等価な代入形式はこちら：

julia> f(x, y) = sqrt(x^2 + y^2) 
f (generic function with 2 methods)

julia> print("結果：", f(3, 4) )
結果：5.0

デフォルト値を持つ引数

 • 関数を定義する段階で、引数のデフォルト値の定義もできる。

 • 引数の初期値・デフォルト値があれば、関数を実行する時にその引数を入力しなくても良い。

function myg(x, y = 1)
    return x^2 + y^2
end
println("myg(2,2) = ", myg(2,2))
println("myg(2) = ", myg(2))

myg(2,2) = 8
myg(2) = 5

---

9. 応用例１：愚数・奇数の数を数える

愚数は　2 で割り切れる整数です。あまり＝０

奇数は　2 で割り切れない整数です。あまり＝１

% はあまりを求める演算子です。

計算例

julia> 4%2
0

julia> 55%2
1

julia> 0%2
0

＊実習課題 3：配列内の要素の分析

 • 次のプログラムを完成させ。

 • プログラムファイル .jl を提出してください。

 • ファイル名に課題番号を記入してください。

 • 出力画面を説明付きで Word に添付してください。

 
function Analyse(A)
    Gusu = 0
    Kisu = 0
    for a in A
        if ❓❓❓
            Gusu += 1
        else
            Kisu += 1
        end
    end
    println("愚数 = $(Gusu) 個")
    println("奇数 = $(Kisu) 個")
end
Analyse(rand(0:10, 100)) #もっと大きい数値を使っても良い

愚数 = 63 個
奇数 = 37 個

---

10. 応用例：ランダムウォーク　Random Walk 2D

 • 別名:乱歩（らんぽ）、酔歩（すいほ）

 • 高分子の幾何学的構造のモデルとして利用されている。

目的：次の　関数を作成する

RandomWalk(N, dTheta = pi/100, R = 1, xo = 0, yo=0)

 • N は 原点も含め、居場所（点）の数です。

 • dTheta 回転角度の刻み。

 • R 一歩の距離。

 • xo と yo ：原点の座標

 • N の入力は必須です。その他の引数が、入力がなけらば既存値を使う。

 • 注意点：「歩数」と「点の数」は同じではない。

出力の例：

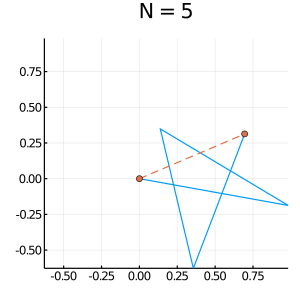
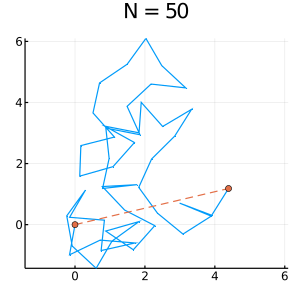
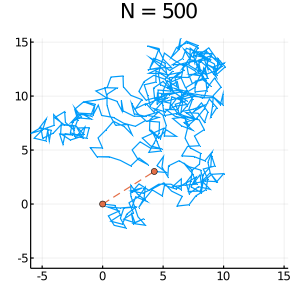
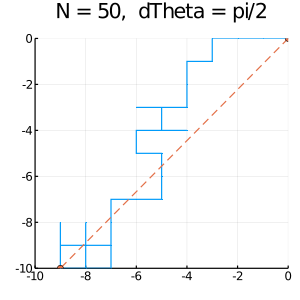
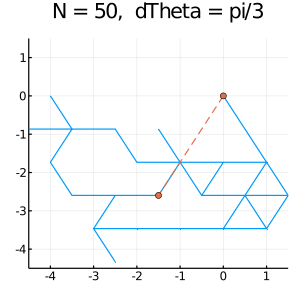
＊実習課題 4：乱歩

 • 上記のグラフを作成するために、下記のプログラムを完成させ。

 • プログラムファイル .jl を提出してください。

 • ファイル名に課題番号を記入してください。

 • プログラムが完成したら, 上記の例みたいに、引数を変えてみて、説明付きでWord にまとめてください。

function RandomWalk(N, dTheta = pi/100, R = 1, xo = 0, yo=0)
    X = zeros(N)
    Y = zeros(N)
    X[1] = xo
    Y[1] = yo
    for n in 1:N-1
        #-pi から piまで、dTheta 刻みで乱数を作成
        theta = rand(-pi: dTheta: pi) 

        dx = R * cos(theta)
        dy = R * sin(theta)
        X[❓] = X[n] + dx
        Y[❓] = Y[n] + dy
    end
    gmax = maximum([maximum(X), maximum(Y)])
    gmin = minimum([minimum(X), minimum(Y)])
    println("最大値 = ", gmax)
    println("最小値 = ", gmin)
    println("始点-終点距離 = ", sqrt((X[end]-xo)^2 + (Y[end]-yo)^2))

    plot(X, Y, legend = false, marker = 1, 
        xlims=(gmin,gmax), ylims = (gmin, gmax)) 
    #始点と終点を繋ぐ
    plot!(X[[1,end]],Y[[1,end]], marker = 4,
        linestyle = :dash, size = (300,300),
        title = "N = $(N)") 
end
RandomWalk(50, pi/100)

---