In the previous chapter, 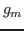 of a MOSFET is considered as constant and
its nonlinearity is ignored. However, drain current of
a MOSFET is represented by
of a MOSFET is considered as constant and
its nonlinearity is ignored. However, drain current of
a MOSFET is represented by
where 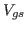 and
and 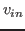 is a gate-to-source bias voltage and
an input signal voltage respectively and
is a gate-to-source bias voltage and
an input signal voltage respectively and 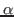 is a coefficient.
The first term of the right side of
Eq. (13) means a constant bias current, the second term is
a desired current which is proportional to the input voltage, and the
last term is a undesired nonlinear components. Only when the input voltage is
sufficiently small to ignore the third term of Eq. (13), a
MOSFET is considered as linear. In order to improve the linearity of
an active inductor, an effect of the third term of Eq. (13)
must be minimize. A variation of the drain-to-source voltage of a MOSFET
also cause distortion. In this paper, only nonlinearity
of
is a coefficient.
The first term of the right side of
Eq. (13) means a constant bias current, the second term is
a desired current which is proportional to the input voltage, and the
last term is a undesired nonlinear components. Only when the input voltage is
sufficiently small to ignore the third term of Eq. (13), a
MOSFET is considered as linear. In order to improve the linearity of
an active inductor, an effect of the third term of Eq. (13)
must be minimize. A variation of the drain-to-source voltage of a MOSFET
also cause distortion. In this paper, only nonlinearity
of 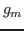 of a MOSFET is discussed because nonlinearity of a
transconductance gives more strong influence on the linearity of a
active inductor.
of a MOSFET is discussed because nonlinearity of a
transconductance gives more strong influence on the linearity of a
active inductor.
Figure 7:
Principle of distortion reduction technique
|
|
Figure 7 shows a basic principle of the proposed
distortion reduction technique. Fig. 7(a) or (b) is used
instead of a n-channel MOSFET which acts as a linear
transconductor. When a drain terminal of the MOSFET is used as an output
terminal, the MOSFET is replaced by Fig. 7(a). When output
node is a source terminal, Fig. 7 (b) is used.
Output current of Fig. 7 is
where 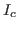 is compensation current. If
is compensation current. If 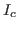 contains the same
nonlinear components with
contains the same
nonlinear components with 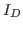 ,
, 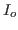 becomes
becomes
where 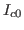 is DC component of
is DC component of 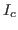 .
The nonlinear components of
.
The nonlinear components of 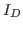 is canceled out. This compensation
current
is canceled out. This compensation
current 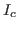 is also realized by a n-channel MOSFET M
is also realized by a n-channel MOSFET M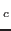 . It is
assumed that M
. It is
assumed that M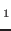 and M
and M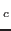 have the same aspect ratio. When
a gate-to-source voltage of M
have the same aspect ratio. When
a gate-to-source voltage of M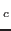 contains
contains  , the drain current
of M
, the drain current
of M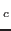 becomes a compensation current.
When gate-to-source voltage of M
becomes a compensation current.
When gate-to-source voltage of M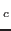 is
is
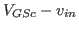 ,
, 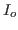 becomes
becomes
A current which is proportional to 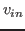 with offset current is
obtained.
with offset current is
obtained.
Takahide Sato
2012-03-31